Distribución t de Student

Distribución t de Student
Distribución t de Student
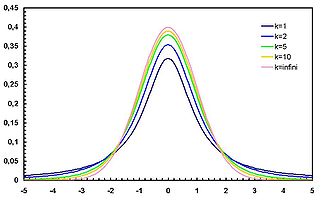
Student densite best.JPG
Función de densidad de probabilidad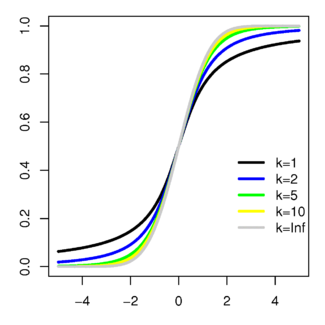
T distributionCDF.png
Función de distribución de probabilidad
Parámetros \nu > 0\! grados de libertad (real)
Dominio x \in (-\infty; +\infty)\!
Función de densidad (pdf) \frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}\!
Función de distribución (cdf) \frac{1}{2} + \frac{x \Gamma \left( (\nu+1)/2 \right) \,_2F_1 \left ( \frac{1}{2},(\nu+1)/2;\frac{3}{2};-\frac{x^2}{\nu} \right)} {\sqrt{\pi\nu}\,\Gamma (\nu/2)} donde \,_2F_1 es la función hipergeométrica
Media 0 para ν > 1, indefinida para otros valores
Mediana 0
Moda 0
Varianza \frac{\nu}{\nu-2}\! para ν > 2, indefinida para otros valores
Coeficiente de simetría 0 para ν > 3
Curtosis \frac{6}{\nu-4}\! para ν > 4
Entropía

\begin{matrix} \frac{\nu+1}{2}\left[ \psi(\frac{1+\nu}{2}) - \psi(\frac{\nu}{2}) \right] \\[0.5em] + \log{\left[\sqrt{\nu}B(\frac{\nu}{2},\frac{1}{2})\right]} \end{matrix}

  • ψ: función digamma,
  • B: función beta
Función generadora de momentos (mgf) (No definida)

En probabilidad y estadística, la distribución t (de Student) es una distribución de probabilidad que surge del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeño.

Aparece de manera natural al realizar la prueba t de Student para la determinación de las diferencias entre dos medias muestrales y para la construcción del intervalo de confianza para la diferencia entre las medias de dos poblaciones cuando se desconoce la desviación típica de una población y ésta debe ser estimada a partir de los datos de una muestra.

Contenido

Caracterización

La distribución t de Student es la distribución de probabilidad del cociente

\frac{Z}{\sqrt{V/\nu\ }}

donde

Si μ es una constante no nula, el cociente \frac{Z+\mu}{\sqrt{V/\nu\ }} es una variable aleatoria que sigue la distribución t de Student no central con parámetro de no-centralidad μ.

Aparición y especificaciones de la distribución t de Student

Supongamos que X1,..., Xn son variables aleatorias independientes distribuidas normalmente, con media μ y varianza σ2. Sea

\overline{X}_n=(X_1+\cdots+X_n)/n

la media muestral. Entonces

Z=\frac{\overline{X}_n-\mu}{\sigma/\sqrt{n}}

sigue una distribución normal de media 0 y varianza 1.

Sin embargo, dado que la desviación estándar no siempre es conocida de antemano, Gosset estudió un cociente relacionado,

T=\frac{\overline{X}_n-\mu}{S_n/\sqrt{n}},

donde

S ^ 2(x) = \frac{1}{n-1} \sum_{i=1}^n (x_i - \overline{x}) ^ 2

es la varianza muestral y demostró que la función de densidad de T es

f(t) = \frac{\Gamma((\nu+1)/2)}{\sqrt{\nu\pi\,}\,\Gamma(\nu/2)} (1+t^2/\nu)^{-(\nu+1)/2}

donde \nu\ es igual a n − 1.

La distribución de T se llama ahora la distribución-t de Student.

El parámetro \nu\ representa el número de grados de libertad. La distribución depende de \nu\ , pero no de μ o σ, lo cual es muy importante en la práctica.

Intervalos de confianza derivados de la distribución t de Student

El procedimiento para el cálculo del intervalo de confianza basado en la t de Student consiste en estimar la desviación típica de los datos S y calcular el error estándar de la media = \frac{S}{\sqrt{n}} , siendo entonces el intervalo de confianza para la media = =\overline{X} \pm t_{\alpha/2,n-1} \frac{S}{\sqrt{n}} .

Es este resultado el que se utiliza en el test de Student: puesto que la diferencia de las medias de muestras de dos distribuciones normales se distribuye también normalmente, la distribución t puede usarse para examinar si esa diferencia puede razonablemente suponerse igual a cero.

para efectos prácticos el valor esperado y la varianza son:

E(t(n))= 0 y Var (t(n-1)) = n/(n-2) para n > 3

Historia

La distribución de Student fue descrita en 1908 por William Sealy Gosset. Gosset trabajaba en una fábrica de cerveza, Guinness, que prohibía a sus empleados la publicación de artículos científicos debido a una difusión previa de secretos industriales. De ahí que Gosset publicase sus resultados bajo el seudónimo de Student.[1]

Referencias

  1. ↑ Walpole, Roland; Myers, Raymond y Ye, Keying (2002). Probability and Statistics for Engineers and Scientists. Pearson Education. 

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Distribución normal — Saltar a navegación, búsqueda Distribución normal Función de densidad de probabilidad La línea verde corresponde a la distribución normal estandar Función de distribución de probabilidad …   Wikipedia Español

  • Distribución χ² — (ji cuadrado) Función de densidad de probabilidad …   Wikipedia Español

  • Distribución de probabilidad continua — Saltar a navegación, búsqueda En Teoría de la probabilidad una distribución de probabilidad se llama continua si su función de distribución es continua. Puesto que la función de distribución de una variable aleatoria X viene dada por , la… …   Wikipedia Español

  • Distribución de Cauchy — Cauchy Lorentz La línea verde es la distribución estándar de Cauchy Función de densidad de probabilidad …   Wikipedia Español

  • Distribución de probabilidad — La distribución Normal suele conocerse como la campana de Gauss . En teoría de la probabilidad y estadística, la distribución de probabilidad de una variable aleatoria es una función que asigna a cada suceso definido sobre la variable aleatoria… …   Wikipedia Español

  • Prueba t de Student — En estadística, una prueba t de Student, prueba t Student, o Test T es cualquier prueba en la que el estadístico utilizado tiene una distribución t de Student si la hipótesis nula es cierta. Se aplica cuando la población se asume ser normal pero… …   Wikipedia Español

  • Función cuantil — En probabilidad la función cuantil de una distribución de probabilidad es la inversa de la función de distribución.[1] Dada una función de distribución continua y estrictamente monótona, , la función cuantil, F −1, devuelve un valor x tal… …   Wikipedia Español

  • William Sealy Gosset — William Sealy Gosset, 1876 1937. William Sealy Gosset (11 de junio de 1876 – 16 de octubre de 1937) fue un estadístico, mejor conocido por su sobrenombre literario Student. Nacido en Canterbury, hijo de Agnes Sealy Vidal y el coronel Frederic… …   Wikipedia Español

  • Estadístico muestral — Saltar a navegación, búsqueda En estadística un estadístico (muestral) es una medida cuantitativa, derivada de un conjunto de datos de una muestra, con el objetivo de estimar o contrastar características de una población o modelo estadístico. Más …   Wikipedia Español

  • Análisis de frecuencia acumulada — La frecuencia acumulada o frecuencia acumulativa es la frecuencia de ocurrencia de valores de un fenómeno menores que un valor de referencia. El fenómeno puede ser un variable aleatoria que varia en el tiempo o en el espacio. La frecuencia… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”