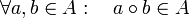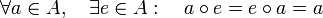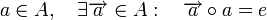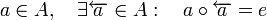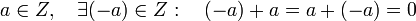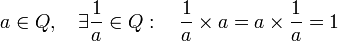- Elemento simétrico
-
Elemento simétrico
En Álgebra abstracta, si tenemos conjunto
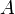 en el que se ha definido una Operación matemática
en el que se ha definido una Operación matemática  , que anotamos:
, que anotamos: 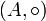 , siendo la operación
, siendo la operación  , interna en
, interna en 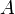 :
:Con elemento neutro
 ,
,Se dice que un elemento
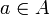 tiene:
tiene:elemento simétrico por la izquierda respecto de la operación
 si:
si:elemento simétrico por la derecha respecto de la operación
 si:
si:elemento simétrico respecto de la operación
 si existe un elemento simétrico por la izquierda y por la derecha, esto es:
si existe un elemento simétrico por la izquierda y por la derecha, esto es:Un elemento simétrico
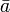 de
de 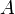 es simétrico por la derecha del elemento
es simétrico por la derecha del elemento 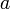 y simétrico por la izquierda del elemento
y simétrico por la izquierda del elemento 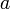 .
.Contenido
Notación
Notación aditiva
Cuando la operación se denota por "+" (más), se denomina suma o adición.
la suma de Número entero: Z, es interna
En ese caso, al elemento neutro se le denomina cero y se le denota por "0",
y al elemento simétrico de
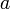 se le denomina elemento opuesto de
se le denomina elemento opuesto de 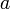 y se le denota por:
y se le denota por: 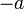 .
.Así partiendo de los números entero: Z, y la operación suma: +, tenemos que:
Notación multiplicativa
Cuando la operación se denota por "·" (por), se denomina producto o multiplicación. La multiplicación de Número racional: Q, es interna
En ese caso, al elemento neutro se le denomina uno o unidad y se le denota por "1":
y al elemento simétrico de
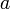 se le denomina elemento inverso de
se le denomina elemento inverso de 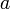 y se le denota por
y se le denota por 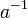 o por
o por 
Partiendo de los números racional: Q y de la operación multiplicación, tenemos:
Véase también
Categorías: Álgebra abstracta | Álgebra elemental
Wikimedia foundation. 2010.