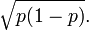- Ensayo de Bernoulli
-
Ensayo de Bernoulli
En la teoría de probabilidad y estadística, un Ensayo de Bernoulli es un experimento, del cual su resultado es aleatorio y puede ser encuadrarse en uno de dos posibles, llamados "éxito" y "fallo".
En la práctica, se refiere a un simple evento que puede tener dos resultados. Estos pueden ser expresados en "Sí" o "No". Por ejemplo:
- Al tirar una moneda, ¿Será cara?
- ¿Era el recién nacido niña?
- ¿Son verdes los ojos de una persona?
- ¿Decidió un cliente potencial, comprar mi producto?
- ¿Un ciudadano votó por un candidato específico?
De ahí que 'éxito ' y 'fallo' son etiquetas para los resultados, y no debe ser interpretado literalmente. Los ejemplos de los Ensayos de Bernoulli incluyen:
- Tirar una moneda. En este contexto, obversa ("cara") convencionalmente denota éxito y el reverso ("sello") denota fallo. Por definición, una moneda tiene 0.5 de probabilidad de éxito.
- Haciendo rodar un dado, en donde por ejemplo designamos un 6 como un "éxito" y todos los demás resultados como "fallo".
- Cuando al conducir una encuesta política, escogiendo al azar un votante para ver si éste votará "si" en un referéndum próximo.
Matemáticamente, tal ensayo es modelado por una variable aleatoria que puede tomar solo dos valores, 0 y 1; siendo 1 el "éxito". Si p es la probabilidad de éxito, entonces el valor del valor esperado de tal variable aleatoria es p y su desviación estándar es
Un proceso de Bernoulli consiste en repetidamente formar independientes pero idénticos ensayos de Bernoulli, por ejemplo tirar 10 veces una moneda
Véase también
Categoría: Teoría de probabilidades
Wikimedia foundation. 2010.