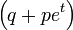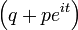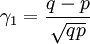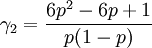- Distribución de Bernoulli
-
Distribución de Bernoulli
Bernoulli Función de distribución de probabilidad Parámetros 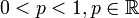
Dominio 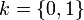
Función de probabilidad (fp) 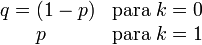
Función de distribución (cdf) 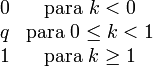
Media 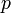
Mediana N/A Moda 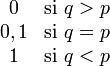
Varianza 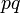
Coeficiente de simetría 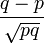
Curtosis 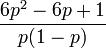
Entropía 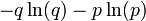
Función generadora de momentos (mgf) 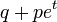
Función característica 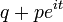
En teoría de probabilidad y estadística, la distribución de Bernoulli (o distribución dicotómica), nombrada así por el matemático y científico suizo Jakob Bernoulli, es una distribución de probabilidad discreta, que toma valor 1 para la probabilidad de éxito (p) y valor 0 para la probabilidad de fracaso (q = 1 − p).
Si X es una variable aleatoria que mide "número de éxitos", y se realiza un único experimento con dos posibles resultados (éxito o fracaso), se dice que la variable aleatoria X se distribuye como una Bernouilli de parámetro p.
X˜Be(p)
La fórmula será:
f(x) = px(1 − p)1 − x con x = {0,1}
Su función de probabilidad viene definida por:
Un experimento al cual se aplica la distribución de Bernoulli se conoce como Ensayo de Bernoulli o simplemente ensayo, y la serie de esos experimentos como ensayos repetidos.
Contenido
Propiedades características
Esperanza matemática:
Varianza:
Función generatriz de momentos:
Función característica:
Moda:
0 si q > p 1 si q < p 0,1 si q = p
Asimetría (Sesgo):Curtosis:
La Curtosis tiende a infinito para valores de p cercanos a 0 ó a 1, pero para
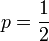 la distribución de Bernoulli tiene un valor de curtosis menor que el de cualquier otra distribución, igual a -2.
la distribución de Bernoulli tiene un valor de curtosis menor que el de cualquier otra distribución, igual a -2.Distribuciones Relacionadas
- Si
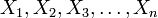 son n variables aleatorias identicamente distribuidas con la distribución de Bernoulli con la misma probabilidad de éxito p en todas, entonces la variable aleatoria
son n variables aleatorias identicamente distribuidas con la distribución de Bernoulli con la misma probabilidad de éxito p en todas, entonces la variable aleatoria 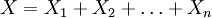 presenta una Distribución Binomial de probabilidad.
presenta una Distribución Binomial de probabilidad.
X˜Bi(n,p)
Ejemplo
"Lanzar una moneda, probabilidad de conseguir que salga cruz".
Se trata de un solo experimento, con dos resultados posibles: el éxito (p) se considerará sacar cruz. Valdrá 0,5. El fracaso (q) que saliera cara, que vale (1 - p) = 1 - 0,5 = 0,5.
La variable aleatoria X medirá "número de cruces que salen en un lanzamiento", y sólo existirán dos resultados posibles: 0 (ninguna cruz, es decir, salir cara) y 1 (una cruz).
Por tanto, la v.a. X se distribuirá como una Bernoulli, ya que cumple todos los requisitos.
X˜Be(0,5)
P(X = 0) = f(0) = 0,500,51 = 0,5
P(X = 1) = f(1) = 0,510,50 = 0,5
Ejemplo:
"Lanzar un dado y salir un 6".
Cuando lanzamos un dado tener 6 posibles resultados:
Ω = {1,2,3,4,5,6}
Estamos realizando un único experimento (lanzar el dado una sola vez).
Se considera éxito sacar un 6, por tanto, la probabilidad según el teorema de Laplace (casos favorables dividido entre casos posibles) será 1/6.
p = 1 / 6
Se considera fracaso no sacar un 6, por tanto, se considera fracaso sacar cualquier otro resultado.
q = 1 − p = 1 − 1 / 6 = 5 / 6
La variable aleatoria X medirá "número de veces que sale un 6", y solo existen dos valores posibles, 0 (que no salga 6) y 1 (que salga un 6).
Por tanto, la variable aleatoria X se distribuye como una Bernoulli de parámetro p = 1/6
X˜Be(1 / 6)
La probabilidad de que obtengamos un 6 viene definida como la probabilidad de que X sea igual a 1.
P(X = 1) = f(1) = (1 / 6)1 * (5 / 6)0 = 1 / 6 = 0.1667
La probabilidad de que NO obtengamos un 6 viene definida como la probabilidad de que X sea igual a 0.
P(X = 0) = f(0) = (1 / 6)0 * (5 / 6)1 = 5 / 6 = 0.8333
Véase también
Categoría: Distribuciones discretas
Wikimedia foundation. 2010.

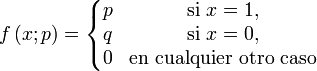
![E\left[X\right] = p](/pictures/eswiki/57/98871c2cbe354046c944e23318038577.png)
![var\left[X\right] = p \left(1 - p\right) = p q](/pictures/eswiki/98/bc80ba4ce849763cc532daedbc7d2f46.png)