Sean 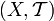espacio topológico, 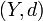espacio métrico, y x₀ un punto en X. Un conjunto H de funciones de X en Y se dice equicontinuo en x₀ si y solamente si para todo 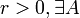entorno de x₀ tal que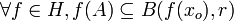

Notar que, en particular, si H es equicontinuo en x₀, entonces todas las funciones que pertenecen a H son continuas en x₀.

Decimos que H es equicontinua si lo es para todo .

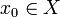Ejemplos

1. Si H es una familia finita de funciones continuas, entonces es equicontinua
2. Si 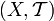es métrico y todas las funciones de H son Lipschitz continuas con una misma constante K, entonces H es equicontinua
3. Si 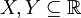, todas las funciones de H son derivables, y existe una constante K > 0 tal que 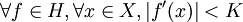, entonces se cumple que todas las funciones de H son Lipschitz continuas de constante K, y, por ende, H es equicontinuo.

Esta última propiedad es una de las más usadas para verificar equicontinuidad de una familia de funciones.