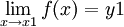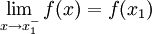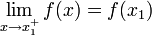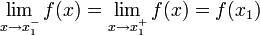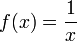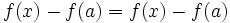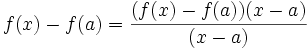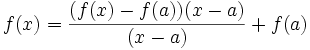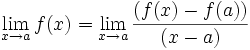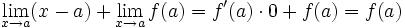- Continuidad (matemática)
-
Continuidad (matemática)
En matemáticas, una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que es discontinua. Generalmente una función continua es aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel.
La continuidad de funciones es uno de los conceptos principales de la topología. El artículo describe principalmente la continuidad de funciones reales de una variable real.
Contenido
- 1 Funciones reales de una variable real
- 2 Funciones continuas en espacios topológicos
- 3 Véase también
Funciones reales de una variable real
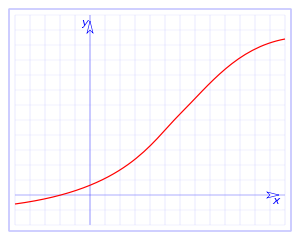
Informalmente hablando, una función f definida sobre un intervalo I es continua si la curva que la representa, es decir el conjunto de los puntos (x, f(x)), con x en I, está constituida por un trazo continuo, es decir un trazo que no está roto, ni tiene "hoyos" ni "saltos", como en la figura de la derecha.
El intervalo I de x es el dominio de definición de f, definido como el conjunto de los valores de x para los cuales f(x) existe.
El intervalo J de y es el rango (también conocido como imagen) de f, el conjunto de los valores de y, tomados como y = f(x). Se escribe J = f(I). Notar que en general, no es igual que el codominio (sólo es igual si la función en cuestión es suprayectiva.)
El mayor elemento de J' se llama el máximo absoluto de f en I, y el menor valor de J es su mínimo absoluto en el dominio I.
Continuidad de una función en un punto
Definición de continuidad en un punto
- Una función f es continua en un punto Xo en el dominio de la función
si
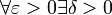 tal que para toda x en el dominio de la función
tal que para toda x en el dominio de la funciónOtra manera mas simple Si Xo es punto de acumulación del dominio de la función entonces f es continua en Xo
- si y sólo si
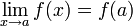
En el caso de aplicaciones de
 en
en  , y de una manera más rigurosa se dice que una función; f es continua en un punto x1 si existe f(x1), si existe el límite de f(x) cuando x tiende hacia x1 por la derecha, si existe el límite de f(x) cuando x tiende hacia x1 por la izquierda, y además coinciden con f(x1).
, y de una manera más rigurosa se dice que una función; f es continua en un punto x1 si existe f(x1), si existe el límite de f(x) cuando x tiende hacia x1 por la derecha, si existe el límite de f(x) cuando x tiende hacia x1 por la izquierda, y además coinciden con f(x1).Así pues, una función f continua en el punto x1 implica lo siguiente:
- Existe f(x1):
- existe el límite por la izquierda:
- existe el límite por la derecha:
- El límite por la derecha por la izquierda y el valor de la función coinciden:
Es decir: el límite de la tasa de variación es cero cuando el incremento de la variable independiente, h, tiende a cero:
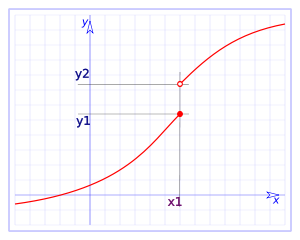
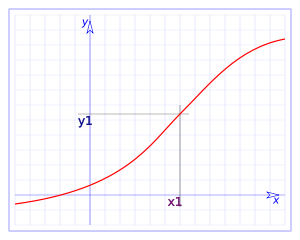
Si f(x1)= y1, la continuidad en x1 se expresa así:
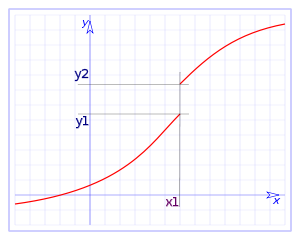
parafraseando, cuando x se aproxima a x1, f(x) se aproxima a y1. Por definición de los límites, esto significa que para todo intervalo abierto J, centrado en y1, existe un intervalo abierto I, centrado en x1, tal que
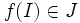 .
.Si f ejecuta un salto en el punto, el teorema cae en falta. En efecto no todo intervalo I alrededor de x1 tiene su imagen en un intervalo J centrado en y1, con un radio inferior al salto de f, no importa lo pequeño que este intervalo sea, hay valores de x del intervalo I alrededor de x1 que tiene su imagen en un intervalo K centrado en y2, siendo y1 y y2 valores distintos, esto es: x tiene imágenes que se salen de J.
La ventaja de esta definición es que se generaliza a cualquier espacio topológico.
Continuidad lateral
Una función f es continua por la izquierda en el punto x = x1 si el límite lateral por la izquierda y el valor de la función en el punto son iguales. Es decir:
como en la figura.
Una función f es continua por la derecha en el punto x = x1 si su límite lateral por la derecha y el valor de la función en el punto son iguales. Es decir:
Una función f es continua en un punto si es continua por la izquierda y es continua por la derecha. Esto es:
Continuidad de una función en un intervalo
Una función, f es continua en un intervalo I, si y solo si la función es continua en todos los puntos del intervalo, es decir:
- f es continua en un intervalo I ⇔
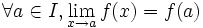
Dado que una función f es continua en un intervalo abierto (a, b) si la función es continua en todos los puntos del intervalo, entonces f es continua en el intervalo cerrado [a, b] si y solo si es continua en el intervalo (a, b) y además es continua en el punto a por la derecha y en el punto b por la izquierda.
La función anterior es continua tanto en [-6, 1) como en (1, 6].
Algunas funciones continuas importantes
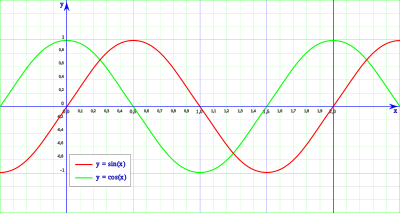
Las funciones polinomiales, trigonométricas: seno y coseno, las exponenciales y los logaritmos son continuas en sus respectivos dominios de definición.
La parábola, como función polinómica, es un ejemplo de función continua a lo largo de todo el dominio real.
En la gráfica se ve la función seno que es periódica, acotada y continua en todo el domino real, dado su carácter periódico, con ver uno solo de los ciclos es suficiente para comprobar la continuidad, porque el resto de los ciclos son exactamente iguales.
Funciones definidas por intervalos
La funciones definidas para distintos intervalos de x, puede ser discontinua en los puntos de cambio de intervalo, como por ejemplo:
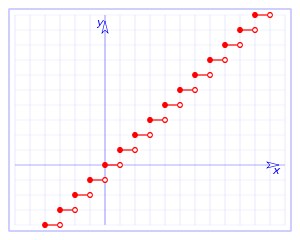
- La Función parte entera de x, E(x), donde E(x) es el mayor número entero inferior o igual a x, tal que:
- E(x) ≤ x < E(x) + 1.
Su curva es una sucesión de segmentos horizontales a distintas alturas. Esta función no es continua en los enteros, pues los límites a la izquierda y a la derecha difieren de uno, pero es continua en los segmentos abiertos (n, n+1) donde es constante.
- Otras funciones definidas por intervalos son:
- Función escalón unitario
- Función signo
Función racional
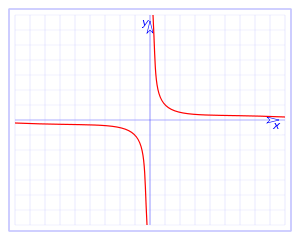
Las funciones racionales son continuas en un intervalo adecuado. Un ejemplo de esto es la función inverso de x:
Esta función es una hipérbola compuesta por dos tramos. x < 0 y x > 0. Como vemos, efectivamente es continua en todo el dominio
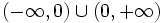 porque no esta definida en x= 0. Si se extiende el dominio de la función a R (dandole un valor arbitrario a f(0)) la función será discontinua.
porque no esta definida en x= 0. Si se extiende el dominio de la función a R (dandole un valor arbitrario a f(0)) la función será discontinua.Derivada y continuidad
Si una función es derivable en x= a entonces es continua en x= a.
Hipótesis: Existe f'(a)
Tesis: f(x) es continua en x= a
Demostración:
Es importante notar que el recíproco no es válido; es decir que nada se puede afirmar sobre la derivabilidad de una función continua. Un ejemplo claro de esta situación es la función valor absoluto f(x)= |x| que si bien es continua en todo su dominio no es derivable en x= 0
Teoremas sobre funciones continuas
Estos son algunos de los teoremas más importantes sobre funciones continuas.
- Teorema de Weierstrass: Si f es continua en [a,b] entonces presenta máximos y mínimos absolutos.
- Teorema de Bolzano: Si f es continua en [a,b] y f(a) > 0 y f(b) < 0, entonces
![\exists c \in ]a,b[](/pictures/eswiki/57/9f565f8f3dfaa671a4b1b3246e2c47d8.png) tal que f(c) = 0
tal que f(c) = 0 - Teorema del valor intermedio: Si f es continua en [a,b] y f(a) < k < f(b) entonces
![\exists c \in ]a,b[](/pictures/eswiki/57/9f565f8f3dfaa671a4b1b3246e2c47d8.png) tal que f(c) = k
tal que f(c) = k
Clase de continuidad
Una función
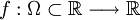 , se dice:
, se dice:- de clase
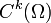 si está definida en todo el dominio Ω junto con sus derivadas hasta orden
si está definida en todo el dominio Ω junto con sus derivadas hasta orden 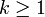 y todas ellas son continuas.
y todas ellas son continuas. - Una función continua aunque no diferenciable en todo el domino, se dice que es de clase
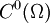 .
. - Una función es de clase
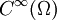 si tiene derivadas continuas de cualquier orden. Aunque muchas sí lo son, no toda función de este tipo es analítica.
si tiene derivadas continuas de cualquier orden. Aunque muchas sí lo son, no toda función de este tipo es analítica. - Una función es de clase
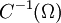 si es la derivada en el sentido de las distribuciones de una función de clase
si es la derivada en el sentido de las distribuciones de una función de clase 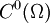 .
. - Una función generalizada se dice de clase
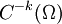 si es la derivada k-ésima en el sentido de las distribuciones de una función de clase
si es la derivada k-ésima en el sentido de las distribuciones de una función de clase 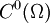 .
.
Funciones continuas en espacios topológicos
Sean (X,TX) e (Y,TY) dos espacios topológicos. Una aplicación
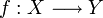 se dice que es continua si:
se dice que es continua si:- f − 1(G) es un abierto de X,
cualquiera que sea el abierto G de Y.
Con la misma notación, si
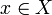 , diremos que f es continua en x cuando se obtiene que f − 1(V) es un entorno de x, cualquiera que sea el entorno V de f(x).
, diremos que f es continua en x cuando se obtiene que f − 1(V) es un entorno de x, cualquiera que sea el entorno V de f(x).Es "inmediato" entonces comprobar que f es continua si y solo si es continua en
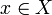 , cualquiera que sea éste, es decir, cuando sea continua en cada uno de los puntos de su dominio.
, cualquiera que sea éste, es decir, cuando sea continua en cada uno de los puntos de su dominio.Véase también
- Discontinuidad
- Función discontinua
- Función
- Límite
- Lista de funciones matemáticas
- Derivación
- Continuo
- Discreto
Categorías: Análisis matemático | Topología | Funciones
Wikimedia foundation. 2010.

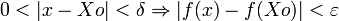
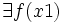
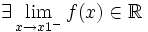
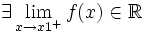
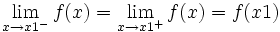
![\lim_{h \to 0} [f(x1+h) - f(x1)] = 0](/pictures/eswiki/101/ea628bf43ee2f21915af3b6b49ee5b44.png)