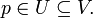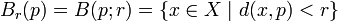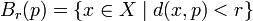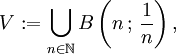Un conjunto V en el plano es un entorno de un punto p si un pequeño disco alrededor de p está contenido en V.

Un rectángulo no es un entorno de ninguna de sus esquinas.

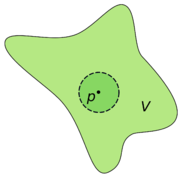
En topología y áreas relacionadas con la matemática, un entorno (o vecindad) es uno de los conceptos básicos de los espacios topológicos. Intuitivamente hablando, un entorno de un punto es un conjunto que contiene al punto en dónde uno puede separarse un poco del punto en cuestión sin abandonar el conjunto.

El concepto de entorno está estrechamente relacionado con los conceptos de conjunto abierto y punto interior.

Definición

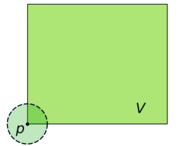
Si X es un espacio topológico y p es un punto perteneciente a X, un entorno de p es un conjunto V que contiene un conjunto abierto U que contiene a p,

Nótese que el entorno V no necesita ser un conjunto abierto. Si V es abierto se lo llama un entorno abierto. Algunos autores especifican que los entornos deben ser abiertos, por lo que es importante prestar cuidado a las diferentes notaciones.

El conjunto de todos los entornos de un punto forma una base de entornos del punto.

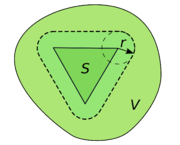
Si S es un subconjunto de X, un entorno de S es un conjunto V, que contiene un conjunto abierto U que contiene a S. Se deduce que un conjunto V es un entorno de S si y solo si es un entorno de todos los puntos de S.

Clases de entorno

• Entorno reducido: un entorno V de un punto a es un entorno reducido si el propio punto a no pertenece al mismo. Es decir, está compuesto solamente por los puntos cercanos a a
• Entornos abiertos: un entorno V de un punto a es entorno abierto de a si V es un conjunto abierto (es decir, ).
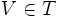• Entornos cerrados: un entorno V de un punto a es entorno cerrado de a si V es un conjunto cerrado.
• Entorno compacto: un entorno V de un punto a es entorno compacto de a si V es un conjunto compacto.
• Entorno conexo: un entorno V de un punto a es entorno conexo de a si V es un conjunto conexo.
• Entorno conexo por caminos: un entorno V de un punto a es entorno conexo por caminos de a si V es un conjunto conexo por caminos.
• Entorno simplemente conexo: un entorno V de un punto a es entorno simplemente conexo de a si V es un conjunto simplemente conexo.
• Entorno convexo: un entorno V de un punto a en un espacio vectorial topológico X es entorno convexo de a si V es un conjunto convexo.

En el espacio métrico

Un conjunto S en el plano y un entorno uniforme V de S.

En un espacio métrico M = (X,d), un conjunto V es un entorno de un punto p si existe una bola abierta con centro p y radio r,

que es contenida en V.

V es llamado entorno uniforme de un conjunto S si existe un número positivo r tal que para todos los elementos p de S,

estén contenidos en V.

Para r>0 el r-entorno S_r de un conjunto S es el conjunto de todos los puntos en X que distan menos de r desde S (o equivalentemente, S_r es la unión de todas las bolas abiertas de radio r que tienen centro en un punto de S).

Se deduce entonces que un r-entorno es un entorno uniforme, y que un conjunto es un entorno uniforme si y solo si contiene un r-entorno para algún valor de r.

Ejemplo

Dado el conjunto de números reales R con la distancia euclideana y un subconjunto V definido como

entonces V es un entorno del conjunto N de números naturales, pero no es un entorno uniforme de este conjunto.

Topología de entornos

La definición superior es útil si la noción de conjunto abierto está previamente definida. Existe una forma alternativa de definir una topología, primeramente definiendo su base de entornos, y entonces los conjuntos abiertos como aquellos conjuntos que contienen un entorno para cada uno de sus puntos.

Una base de entornos en X es la asignación de un filtro N(x) (en el conjunto X) para cada x en X tal que:

1. el punto x es un elemento de cada U en N(x).
2. cada U en N(x) contiene algún V en N(x) tal que para cada y en V, U esté en N(y).

Entorno uniforme

En un espacio uniforme S:=(X, δ) V es denominado entorno uniforme de P si P no es cercano a X \ V, tal que allí no exista un espacio uniforme que contenga a P y X \ V.

Entorno reducido

Un entorno reducido de un punto p es un entorno de p, menos {p}. Por ejemplo, el intervalo (−1, 1) = {y : −1 < y < 1} es un entorno de p = 0 en la recta real, entonces el conjunto (−1, 0) ∪ (0, 1) = (−1, 1) − {0} es un entorno reducido de 0.

Véase además

• Base de entornos
• Continuidad (matemática)
• Teoría de conjuntos

Referencias

• Kelley, John L. (1975). General topology. New York: Springer-Verlag. ISBN 0387901256.

• Bredon, Glen E. (1993). Topology and geometry. New York: Springer-Verlag. ISBN 0387979263.

• Kaplansky, Irving (2001). Set Theory and Metric Spaces. American Mathematical Society. ISBN 0821826948.