Función digamma

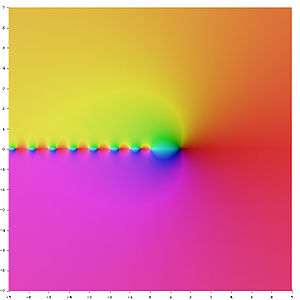Función digamma
Función Digamma Ψ(s) en el plano complejo. El color de un punto s codifica el valor de Ψ(s).Colores fuertes denotan valores cercanos a cero y el tono codifica el valor del argumento.

En matemáticas, la función digamma se define como la derivada logarítmica de la función gamma, siendo la primera de las funciones poligamma. Se define de la siguiente manera:

\psi(z) =\frac{d\,\ln\Gamma}{dz}(z)= \frac{\Gamma'(z)}{\Gamma(z)}

donde Γ denota la función gamma.

Contenido

Representaciones

Usando la expresión

\Gamma(z) = \frac{e^{-\gamma z}}{z}\prod_{n=1}^\infty \left(1 + \frac{z}{n}\right)^{-1} e^{z/n},

donde γ es la constante de Euler-Mascheroni, podemos tomar el logaritmo

\ln(\Gamma(z)) = -\gamma z - \ln z - \sum_{n=1}^\infty \ln\left(1 + \frac{z}{n}\right) - z/n

y derivando respecto de z, obtenemos una representación en forma de serie

\psi(z) = -\gamma - \frac{1}{z} + \sum_{n=1}^\infty \left(\frac{1}{n} - \frac{1}{n+z}\right) = -\gamma + \sum_{k=1}^\infty \left( \frac{1}{k}-\frac{1}{z+k-1} \right).

Propiedades

De la expresión anterior se desprende la relación de recurrencia

\psi(z + 1) = \psi(z) + \frac{1}{z}.

De aquí que si n es un entero positivo, entonces

\psi(n) = -\gamma + \sum_{k=1}^{n-1}\frac{1}{k} = -\gamma + H_{n-1}

donde Hn − 1 es el (n − 1)-ésimo número armónico.

\Psi(1 - x) - \Psi(x) = \pi\,\!\cot{ \left ( \pi x \right ) }
  • La función digamma tiende asintóticamente a la función logaritmo.
  • La función digamma también se denota como ψ0(x) o incluso ψ0(x).

Temas relacionados

Referencias

  • Abramowitz, M. and Stegun, I. A. (Eds.). "Psi (Digamma) Function." §6.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 258-259, 1972. See section §6.4
  • Weisstein, Eric W. «Digamma function» (en inglés). MathWorld. Wolfram Research.

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Función digamma — En matemáticas, la función digamma se define como: donde D es el operador diferencial. La función digamma, que también se denota como ψ0(x) o incluso ψ0(x), está relacionada con los números armónicos en que donde H …   Enciclopedia Universal

  • Función gamma — en el eje real. Valor absoluto de la función gamma en el plano complejo …   Wikipedia Español

  • Función poligamma — Diferentes gráficas de la función poligamma a lo largo del eje x. En naranja, para m=0, en amarillo, para m=1, en verde, para m=2, en rojo, para m=3 y en azul para m=4. En matemática, la función poligamma de orden m se define como la m ésima… …   Wikipedia Español

  • Función beta — Este artículo trata sobre función beta de Euler. Para otras funciones beta, véase Función beta (desambiguación). Función beta. Representación de la función para valores reales positivos de x e y. En matemáticas, la función beta …   Wikipedia Español

  • Función trigamma — Este artículo trata sobre la función trigamma. Para la función gamma triple, véase función gamma de Barnes. Trigamma function ψ1(z) in the complex plane. The color of a point z encodes the value of ψ1(z). Strong colors denote values close to zero …   Wikipedia Español

  • Función zeta de Hurwitz — En matemáticas, la función zeta de Hurwitz es una de las muchas funciones zetas. Se la define formalmente para un argumento complejo s y un argumento real q como Esta sucesión es convergente para q > 0 y Re(s) > 1. Si q… …   Wikipedia Español

  • Función poligamma — En matemáticas, la función poligamma de orden m se define como: donde es la función digamma …   Enciclopedia Universal

  • Número armónico — El número armónico Hn,1 con (gráfica roja) con su límite asintótico γ + log x (gráfica azul). En matemáticas, se define el n ésimo número armónico como la suma de los recíprocos de los primeros n …   Wikipedia Español

  • Constante de Euler-Mascheroni — La constante de Euler Mascheroni, (también conocida como constante de Euler ) es una constante matemática que aparece principalmente en teoría de números, y se denota con la letra griega minúscula γ (Gamma). Se define como el límite de la… …   Wikipedia Español

  • Ψ — Letras griegas Α α Alfa Β β Beta Γ γ Gamma Δ δ Delta Ε ε Épsilon Ζ ζ Dseda Η η Eta …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”