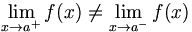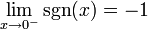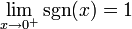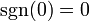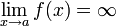Función discontinua

Función discontinua

Función discontinua

Una función es una función discontinua si no es continua en un punto evaluado.

Contenido

Clasificación de la discontinuidad de una función

La discontinuidad de una función puede ser clasificada en:

Discontinuidad { \color{Red} \left \{ \begin{array}{l} Evitable \\ Esencial { \color{PineGreen} \left \{ \begin{array}{l} De \; primera \; especie { \color{Blue} \left \{ \begin{array}{l} De \; salto \; finito \\ De \; salto \; infinito \end{array} \right . }\\ \\ De \; segunda \; especie \end{array} \right . } \\ \end{array} \right . }

Evitable

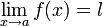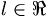Cuando existe el \lim_{x \to a} f(x) = l con l \in \real pero no coincide con el valor de f (a) ya sea porque son distintos los valores o no existe f (a).

Ejemplo 1:
Dada 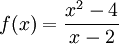f(x) = \frac {x^2-4} {x-2} no existe f(2) pero si existe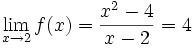
\lim_{x \to 2}f(x) = \frac {x^2-4} {x-2} = 4

Esencial

Cuando se produce algunas de las siguientes situaciones:

  1. Existen los límites laterales pero no coinciden.
  2. Alguno de los límites laterales o ambos son infinitos. Ver asíntota.
  3. No existe alguno de los límites laterales o ambos.
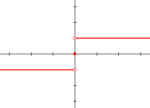
De primera especie o de salto
Con salto finito

Cuando existe el límite por la derecha y por la izquierda (siendo ambos finitos) pero no coinciden.

Signum.png
\lim_{x \to a^+} f(x) \ne \lim_{x \to a^-} f(x)
Ejemplo: La función signo
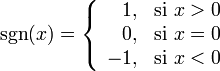
\sgn (x) = \left\{ \begin{array}{rl} 1, & \mbox{si }x > 0 \\ 0, & \mbox{si }x = 0 \\ -1, & \mbox{si }x < 0 \end{array} \right.
\lim_{x \to 0^-} \sgn(x) = -1
\lim_{x \to 0^+} \sgn(x) = 1

y además:

\sgn(0) = 0 \,
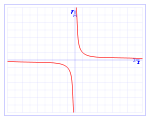
Con salto infinito (asíntota)

Cuando alguno de los límites laterales o ambos no es finito. Puede ser asintótica por la derecha, por la izquierda o por ambos lados.

Función Continua 033.svg
\lim_{x \to a} f(x) = \infty
Ejemplo:
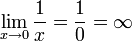
\lim_{x \to 0} \frac {1}{x} = \frac {1}{0} = \infty
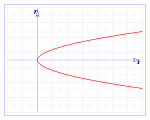
De segunda especie
Función Continua 044.svg

Este tipo de discontinuidad se produce cuando no existe uno de los límites laterales, o ambos.

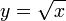
Ejemplo: la función Raíz cuadrada: y = \sqrt {x}

Véase también

Obtenido de "Funci%C3%B3n discontinua"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Función discontinua — Una función es discontinua si no es continua en ese punto …   Enciclopedia Universal

  • Función — (Del lat. functio, onis.) ► sustantivo femenino 1 BIOLOGÍA Actividad o capacidad de acción específica de un ser vivo y de sus órganos: ■ la función del riñón; la función clorofílica. 2 Desempeño de un cargo u oficio: ■ el vicepresidente desempeña …   Enciclopedia Universal

  • Función unitaria de Heaviside — La función escalón de Heaviside, también llamada función escalón unitario, debe su nombre al matemático inglés Oliver Heaviside. Es una función discontinua cuyo valor es 0 para cualquier argumento negativo, y 1 para cualquier argumento positivo:… …   Wikipedia Español

  • Función discreta — Una función discreta es una función matemática cuyo dominio de definición es un conjunto numerable (o discreto).[1] Es decir, es una definición: Una función discreta no debe confundirse con una función discontinua, puesto que estas últimas… …   Wikipedia Español

  • Función continua — En matemáticas, una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que es discontinua. Generalmente… …   Wikipedia Español

  • Función polilogarítmica — El polilogaritmo (también conocido como función de Jonquière) es una función especial definida por la siguiente serie: Esta no es, en general, una función elemental, aunque esté relacionada con la función logarítmica. La definición dada arriba es …   Wikipedia Español

  • Gráfica de una función — En matemáticas, la gráfica de una función: es la visualización de la correspondencia entre los elementos del conjunto dominio y los del conjunto imagen mediante su representación iconográfica. También puede definirse como el conjunto formado por… …   Wikipedia Español

  • Continuidad (matemática) — Saltar a navegación, búsqueda En matemáticas, una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que… …   Wikipedia Español

  • Teoría de distribuciones — En Análisis matemático una distribución, también llamada función generalizada, es un objeto matemático que generaliza la noción de función y la de medida. Además la noción de distribución sirve para extender el concepto de derivada a todas las… …   Wikipedia Español

  • Teoría de las tres fases del tráfico — La Teoría de las tres fases del tráfico fue desarrollada por Boris Kerner entre 1996 y 2002.[1] [2] [3] En ella se presenta un nuevo enfoque para el fenómeno del colapso del tráfico, entendiéndose como colapso a la repentina degradación de la… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”