Hamiltoniano (mecánica clásica)

Hamiltoniano (mecánica clásica)
Para la versión cuántica del Hamiltoniano, véase Hamiltoniano (mecánica cuántica).

El hamiltoniano es una función escalar a partir de la cual pueden obtenerse las ecuaciones de movimiento de un sistema mecánico clásico que se emplea en el enfoque hamiltoniano de la mecánica clásica.

Bajo ciertas condiciones relacionadas con las características del sistema (sistema conservativo) y las coordenadas empleadas, el hamiltoniano puede identificarse con la energía mecánica del sistema, aunque esto no sucede para todos los sistemas.

Usualmente el hamiltoniano es una función de las variables de posición y sus momentos conjugados, o más generalmente puede definirse como una función escalar definida sobre el espacio fásico del sistema.

Contenido

Hamiltoniano clásico

Hamiltoniano y energía

Fijado un conjunto de coordenadas canónicas sobre el espacio de fases de un sistema hamiltoniano (con un número finito de grados de libertad), el hamiltoniano o función hamiltoniana puede representarse por una función de las coordenadas generalizadas y los correspondientes momentos conjugados:

(\mathbf{q},\mathbf{p},t)\in \mathbb{R}^{2n+1} \mapsto H(\mathbf{q},\mathbf{p},t)\in \mathbb{R}

Si el sistema es autónomo, es decir, si no existe dependencia explícita del tiempo t en el lagrangiano y el conjunto de coordenadas escogidas son naturales, entonces puede probarse que el hamiltoniano es una integral de movimiento y además coincide en valor con la energía mecánica total del sistema.

  • Para mostrar que el hamiltoniano es una constante del movimiento para un sistema autónomo, lo escribimos en términos del lagrangiano y calculamos su derivada total respecto al tiempo:

H = \mathbf{p}\mathbf{\dot q}-L \qquad \Rightarrow \qquad \frac{dH}{dt} = \mathbf{\dot p}\mathbf{\dot q} + \mathbf{p}\mathbf{\ddot q} - \frac{\part L}{\part \mathbf{\dot q}}\mathbf{\ddot q} - \frac{\part L}{\part \mathbf{q}}\mathbf{\dot q} -\frac{\part L}{\part t}

Teniendo en cuenta las ecuaciones de Euler-Lagrange y relación entre velocidades y la definición de momentos conjugados, se tiene finalmente que la derivada total del hamiltoniano coincide con la derivada parcial de lagrangiano, por lo que, si éste no depende explícitamente del tiempo, el hamiltoniano es constante, ya que:[1]

\frac{dH}{dt} = \mathbf{\dot p}\mathbf{\dot q} + \mathbf{p}\mathbf{\ddot q} - (\mathbf{p})\mathbf{\ddot q} - (\mathbf{\dot p})\mathbf{\dot q} -\frac{\part L}{\part t} = 0 + 0 -\frac{\part L}{\part t}

  • Para ver si el sistema es natural, es decir, si el hamiltoniano coincide con la energía, se calcula la energía cinética expresada en las coordenadas generalizadas a partir de su expresión newtoniana:[2]

E_c =\sum_i \frac{1}{2}m_i\mathbf{\dot r}_i(q_j,t) = \left(\sum_j \frac{1}{2}A_{jk}\dot{q}_j\dot{q}_k \right) + \left(\sum_j B_j\dot{q}_j \right) + C = T_2 + T_1 + T_0

Donde:
T_2\, son los términos cuadráticos en las velocidades.
T_1\, son los términos lineales en las velocidades.
T_0\, son los términos no dependientes de la velocidad.
A_{jk} = \sum_i m_i \frac{\part \mathbf{r}_i}{\part q_j}\frac{\part \mathbf{r}_i}{\part q_k} \quad B_j = \sum_i m_i \frac{\part \mathbf{r}_i}{\part q_j}\frac{\part \mathbf{r}_i}{\part t} \quad C = \frac{1}{2} \sum_i m_i \left(\frac{\part \mathbf{r}_i}{\part t}\right)^2
La energía mecánica total (energía cinética (Ec)+ energía potencial (Ep)) y el hamiltoniano no coincidirán a menos que T0 = 0, y en ese caso general:

H = \mathbf{\dot q}\frac{\part L}{\part \mathbf{\dot q}} - L = (2T_2 + T_1) - (T_2+T_1+T_0 -E_p) = T_2 -T_0 + E_p \ne E_c + E_p

Sin embargo, el sistema será natural si T1 = T0 = 0(Bj = 0, C = 0) y si la energía mecánica total y el hamiltoniano coinciden.

Integral de Jacobi-Painlevé

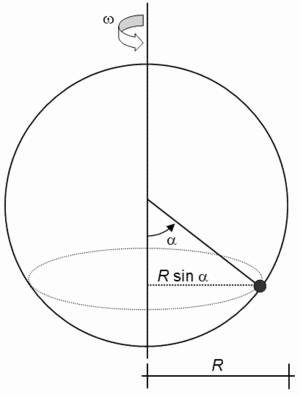Péndulo esférico con rotación uniforme forzada.

En un sistema autónomo, en el que el lagrangiano no depende del tiempo, el hamiltoniano sigue siendo una integral del movimiento y por tanto se mantiene constante. En la sección anterior vimos que este valor constante es igual a:

I_{JP}= H = T_2 -T_0 + E_p\;

Este valor, para sistemas autónomos es lo que se conoce como integral de Jacobi o integral de Jacobi-Painlevé. Conviene notar, sin embargo, que si el sistema no es natural este valor constante del hamiltoniano en general no coincidirá con el valor total de la energía mecánica y por tanto la energía mecánica no tiene por qué ser una constante del movimiento, ya que ésta viene dada por:

E_m = E_c +E_p = T_2 +T_1 + T_0 + E_p\;

Un péndulo esférico es un caso de sistema no-natural y simultáneamente autónomo. El lagrangiano de un péndulo forzado, como el de la figura, formado por una partícula de masa m sujeta a un hilo inextensible forzado a girar con velocidad angular ω mientras oscila respecto a un eje perpendicular a la dirección:

L = \frac{1}{2}mR^2(\dot{\alpha}^2 + \omega^2\sin^2\alpha) - mgR(1-\cos\alpha)

Obviamente este lagrangiano es independiente del tiempo, por lo que el sistema es autónomo; sin embargo, la relación entre la coordenada generalizada α y las coordenadas cartesinas de la partícula son relaciones dependientes del tiempo:

\begin{cases}x = f_1(\alpha,t) = & -R\cos \alpha\cos \omega t \\ y= f_2(\alpha,t) = & -R\cos \alpha\sin \omega t\\ z= f_3(\alpha) = & -R\cos \alpha \end{cases}

Puesto que esas relaciones dependen explícitamente del tiempo, el sistema de coordenadas generalizadas no es natural. El hamiltoniano, por no depender el lagragiano del tiempo, es obviamente una magnitud conservada o constante del movimiento:

H = \frac{1}{2}mR^2(\dot\alpha^2- \omega^2\sin^2\alpha) + mgR(1-\cos\alpha)

Sin embargo, la energía mecánica del sistema, suma de la energía cinética y la energía potencial, es en este caso:

E_m = E_c + E_p = \frac{1}{2}mR^2(\dot\alpha^2+ \omega^2\sin^2\alpha) + mgR(1-\cos\alpha)

La explicación de por qué no se conserva es simple. El sistema, aunque autónomo, no está aislado, pues necesita un "motor" que mantenga constante la velocidad angular ω. Por ello hay un flujo de energía desde el exterior, y la energía mecánica oscila entre un máximo y un mínimo. El valor instantáneo de la energía y su valor medio temporal son:

E_m(t) = H + mR^2\omega^2\sin^2\alpha(t), \qquad \bar{E}_m = H + \frac{mR^2\omega^2}{2}

Ejemplos

H(\bold{r},\bold{\dot r}) = \frac{1}{2}m \bold{\dot r}^2 + \phi(\bold{r})

Casos particular del anterior son:

H(\theta,\dot\theta) = \frac{1}{2}mL^2 \dot\theta^2 + mgL(1-\cos \theta)

H(\theta, \phi, \dot\theta, \dot\phi) = \frac{1}{2}mL^2(\dot{\theta}^2+ \dot{\phi}^2\sin^2\theta) - mgL\cos\theta

Hamiltoniano cuántico

Artículo principal: Hamiltoniano (mecánica cuántica)

En mecánica cuántica se usa un concepto de hamiltoniano diferente matemáticamente del usado en mecánica clásica. Si bien en mecánica clásica el hamiltoniano es una función definida sobre el espacio de fases del sistema (variedad simpléctica de dimensión finita), en mecánica cuántica el hamiltoniano es un operador lineal que actúa sobre elementos de un espacio vectorial, generalmente de dimensión infinita.

La conexión entre ambos conceptos es difícil de entender. Para empezar, necesitamos definir una medida invariante sobre el espacio de fases que usualmente se toma como una potencia de la forma simpléctica que define la estructura simpléctica de dicho espacio:

\forall C\ \mbox{medible}\subset \mathcal{M}: \mu(C):= \int_C \eta_\Gamma = \int_C \bigwedge_{i=1}^n \omega = \int_C \omega\land\dots\land\omega

Donde \eta_\Gamma\; es la medida invariante que aparece en el teorema de Liouville. Además, la solución de las ecuaciones de Hamilton dan lugar a un flujo sobre el espacio fásico, que puede representarse por un grupo uniparamétrico {Tt}. Finalmente, puede verse que este flujo induce sobre las funciones de cuadrado integrable definidas un grupo unitario de operadores de evolución {Ut}:

(*) \langle U^tf, U^tg\rangle = \int_\mathcal{M} f(T^tx)g(T^tx) d^n\omega = \langle f, g\rangle

Esta última idea se corresponde bastante bien con la idea de la función de ondas de un sistema cuántico, y se puede representar en muchos casos como una función de cuadrado integrable sobre el espacio de posiciones de la partícula. La ecuación de la solución de Schrödinger puede representarse también por un grupo unitario de operadores construible a partir del hamiltoniano cuántico:

(**) |\Psi_t\rangle = \hat{U}^t|\Psi_0\rangle = e^{i\hat{H}t/\hbar}|\Psi_0\rangle \quad \Rightarrow \quad \langle \Phi_t|\Psi_t\rangle = \langle \hat{U}^t\Phi_0| \hat{U}^t\Phi_0\rangle = \langle \Phi_0|\Psi_0\rangle

Los parelelos formales entre (*) y (**) son evidentes.

Referencias

  1. ↑ Landau & Lifshitz, p.159
  2. ↑ Fernández Rañada, p.106.

Bibliografía

  • Landau, L.D.; Lifshitz E.M.. «VII». En Reverté. Mecánica (2ª edición). Barcelona. pp. 158-189. ISBN 84-291-4080-6. 
  • Fernádez Rañada, Antonio. Fondo de Cultura Económica. ed. Dinámica Clásica (1ª edición). México DF. pp. 77-131. ISBN 84-206-8133-4. 

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Hamiltoniano (mecánica cuántica) — El Hamiltoniano H tiene dos significados distintos, aunque relacionados. En mecánica clásica, es una función que describe el estado de un sistema mecánico en términos de variables posición y momento, y es la base para la reformulación de la… …   Wikipedia Español

  • Mecánica clásica — El Sistema Solar puede ser explicado con gran aproximación mediante la mecánica clásica, concretamente, mediante las leyes de Newton y la ley de la gravitación universal de Newton. Sólo algunas pequeñas desviaciones en el perihelio de mercurio… …   Wikipedia Español

  • Hamiltoniano (mecánica cuántica) — El Hamiltoniano H tiene dos significados distintos, aunque relacionados. En mecánica clásica, es una función que describe el estado de un sistema mecánico en términos de variables posición y momento, y es la base para la reformulación de la… …   Enciclopedia Universal

  • Hamiltoniano molecular — Este artículo o sección necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 14 de septiembre de 2011. También puedes ayudar… …   Wikipedia Español

  • Mecánica hamiltoniana — La mecánica hamiltoniana fue formulada en 1833 por William R. Hamilton. Como la mecánica lagrangiana, es una reformulación de la mecánica clásica. La mecánica hamiltoniana puede ser formulada por sí misma, usando los espacios simplécticos, sin… …   Wikipedia Español

  • Mecánica matricial — La Mecánica matricial es una formulación de la mecánica cuántica creada por Werner Heisenberg, Max Born y Pascual Jordan en 1925. La mecánica matricial fue la primera definición completa y correcta de la mecánica cuántica. Extiende el modelo de… …   Wikipedia Español

  • Mecánica analítica — La mecánica analítica es una formulación abstracta y general de la mecánica,[1] que permite el uso en igualdad de condiciones de sistemas inerciales o no inerciales sin que, a diferencia de las leyes de Newton, la forma básica de las ecuaciones… …   Wikipedia Español

  • Mecánica cuántica — Imagen ilustrativa de la dualidad onda partícula, en el cual se puede ver cómo un mismo fenómeno puede tener dos percepciones distintas. La mecánica cuántica[1] [2] es …   Wikipedia Español

  • Mecánica lagrangiana — La mecánica lagrangiana es una reformulación de la mecánica clásica introducida por Joseph Louis Lagrange en 1788. En la mecánica lagrangiana, la trayectoria de un objeto es obtenida encontrando la trayectoria que minimiza la acción, que es la… …   Wikipedia Español

  • Operador (mecánica cuántica) — Se ha sugerido que este artículo o sección sea fusionado en observable (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí. El operador cuántico es el operador matemático que representa a una… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”