Hipérbola

Hipérbola
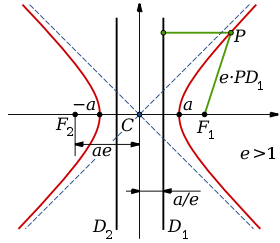Las asíntotas de la hipérbola se muestran como líneas discontinuas azules que se cortan en el centro de la hipérbola (curvas rojas), C. Los dos puntos focales se denominan F1 y F2, la línea negra que los une es el eje transversal. La delgada línea perpendicular en negro que pasa por el centro es el eje conjugado. Las dos líneas gruesas en negro paralelas al eje conjugado (por lo tanto, perpendicular al eje transversal) son las dos directrices, D1 y D2. La excentricidad e (e>1), es igual al cociente entre las distancias (en verde) desde un punto P de la hipérbola a uno de los focos y su correspondiente directriz. Los dos vértices se encuentran en el eje transversal a una distancia ±a con respecto al centro.

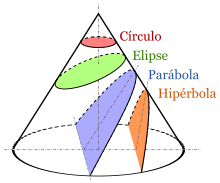
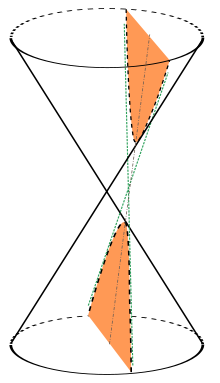
Una hipérbola (del griego ὑπερβολή) es una sección cónica, una curva abierta de dos ramas obtenida al cortar un cono recto por un plano oblicuo al eje de simetría con ángulo menor que el de la generatriz respecto del eje de revolución.[1]

Una hipérbola es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.

Contenido

Etimología. Hipérbole e hipérbola

Secciones cónicas.

Hipérbola deriva de la palabra griega ὑπερβολή (exceso), y es cognado de hipérbole (la figura literaria que equivale a exageración).

Véase también: hipérbole

Historia

Debido a la inclinación del corte, el plano de la hipérbola interseca ambas ramas del cono.

Según la tradición, las secciones cónicas fueron descubiertas por Menecmo, en su estudio del problema de la duplicación del cubo,[2] donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes.[3]

Sin embargo, el primero en usar el término hipérbola fue Apolonio de Perge en su tratado Cónicas,[4] considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.

Ecuaciones de la hipérbola

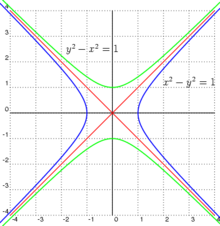
Ecuaciones en coordenadas cartesianas: Ecuación de una hipérbola con centro en el origen de coordenadas (0, 0) \, y ecuación de la hipérbola en su forma canónica.

\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1

Ecuación de una hipérbola con centro en el punto (h, k) \,

\frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1

Ejemplos:

a)

\frac{(x)^2}{25} - \frac{(y)^2}{9} = 1

b)

\frac{(x)^2}{9} - \frac{(y)^2}{25} = 1

Si el semieje transverso a se encuentra en el eje x, y el semieje conjugado b, en el eje y, entonces la hipérbola es horizontal; si es al revés, es vertical. La excentricidad de una hipérbola siempre es mayor que uno.


Ecuación de la hipérbola en su forma compleja

Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos z\,, en el plano Re Im\,; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias |z-w_1|-|z-w_2|\,, a dos puntos fijos llamados focosw_1\, y w_2\,, es una constante positiva igual al doble de la distancia (o sea 2l\, ) que existe entre su centro y cualesquiera de sus vértices del eje focal.

La ecuación queda: |z-w_1|-|z-w_2|=2l\,

Evidentemente esta operación se lleva a cabo en el conjunto de los números complejos.

Ecuaciones en coordenadas polares

Dos hipérbolas y sus asíntotas.

Hipérbola abierta de derecha a izquierda: Hyperbola2.png

r^2 =a\sec 2\theta \,


Hipérbola abierta de arriba a abajo:

r^2 =-a\sec 2\theta \,

Hipérbola abierta de noreste a suroeste: Giperbola-ravnoboch.png

r^2 =a\csc 2\theta \,

Hipérbola abierta de noroeste a sureste:

r^2 =-a\csc 2\theta \,

Ecuaciones paramétricas

Imagen de sección cónica.

Hipérbola abierta de derecha a izquierda:

\begin{matrix} x = a\sec t + h \\ y = b\tan t + k \\ \end{matrix} \qquad \mathrm{o} \qquad\begin{matrix} x = \pm a\cosh t + h \\ y = b\sinh t + k \\ \end{matrix}

Hipérbola abierta de arriba a abajo:

\begin{matrix} x = a\tan t + h \\ y = b\sec t + k \\ \end{matrix} \qquad \mathrm{o} \qquad\begin{matrix} x = a\sinh t + h \\ y = \pm b\cosh t + k \\ \end{matrix}

En todas las formulas (h,k) son las coordenadas del centro de la hipérbola, a es la longitud del semieje mayor, b es la longitud del semieje menor.

Véase también

Referencias

  1. ↑ Si el ángulo de plano intersección, respecto del eje de revolución, es mayor que el comprendido entre la generatriz y el eje de revolución, la intersección será una elipse. Será una parábola si es paralelo al citado eje, y una circunferencia si es perpendicular al eje.
  2. ↑ Heath, Sir Thomas (1921) (en inglés). A history of Greek Mathematics vol. 1. Londres, Inglaterra: Oxford University Press. OCLC 2014918. 
  3. ↑ Ken Schmarge. «Conic Sections in Ancient Greece» (en inglés). Consultado el 02-06-2008 de 2008.
  4. ↑ J. J. O'Connor y E. F. Robertson. «Apollonius of Perga» (en inglés). Consultado el 02-06-2008.

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • hiperbolă — HIPÉRBOLĂ, hiperbole, s.f. 1. (mat.) Curbă reprezentând locul geometric al punctelor dintr un plan pentru care diferenţa distanţelor faţă de două puncte fixe, numite focare, este constantă. 2. Figură de stil care constă în exagerarea mărimii,… …   Dicționar Român

  • hipèrbola — ž 1. {{001f}}jez. knjiž. stilska figura koja se sastoji u uporabi pretjeranih izraza; preuveličavanje, pretjerivanje 2. {{001f}}mat. ravninska krivulja sa svojstvom da je apsolutna vrijednost razlike udaljenosti svake njezine točke od dva zadana… …   Veliki rječnik hrvatskoga jezika

  • hiperbola — hipèrbola ž DEFINICIJA 1. jez. knjiž. stilska figura koja se sastoji u uporabi pretjeranih izraza; pretjerivanje, preuveličavanje 2. mat. ravninska krivulja sa svojstvom da je apsolutna vrijednost razlike udaljenosti svake njezine točke od dva… …   Hrvatski jezični portal

  • hiperbola — {{/stl 13}}{{stl 8}}rz. ż IIa, lm D. hiperbolali || hiperbolabol {{/stl 8}}{{stl 20}} {{/stl 20}}{{stl 12}}1. {{/stl 12}}{{stl 8}}lit. {{/stl 8}}{{stl 7}} środek stylistyczny polegający na wyolbrzymieniu cech opisywanego zjawiska lub przedmiotu,… …   Langenscheidt Polski wyjaśnień

  • hipérbola — sustantivo femenino 1. Área: geometría Curva plana y simétrica que resulta de cortar una superficie cónica por un plano paralelo a su eje …   Diccionario Salamanca de la Lengua Española

  • hipérbola — (Del lat. hyperbŏla, y este del gr. ὑπερβολή). f. Geom. Lugar geométrico de los puntos de un plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante. Resulta de cortar un cono circular por un plano que encuentra a todas …   Diccionario de la lengua española

  • Hipérbola — (Del gr. hyperbole, exceso.) ► sustantivo femenino 1 GEOMETRÍA Curva simétrica y plana que se obtiene cortando una superficie cónica por un plano paralelo a su eje. FRASEOLOGÍA hipérbolas conjugadas GEOMETRÍA Las que tienen las mismas asíntotas y …   Enciclopedia Universal

  • hiperbola — ż I, DCMs. hiperbolali; lm D. hiperbolaol a. hiperbolali 1. lit. «zwrot stylistyczny polegający na zamierzonej przesadzie w opisie przedmiotu lub zjawiska (np. morze krwi, oszalały z gniewu)» Posługiwać się hiperbolami. Wyrazić coś za pomocą… …   Słownik języka polskiego

  • hipérbola — {{＃}}{{LM H20307}}{{〓}} {{［}}hipérbola{{］}} ‹hi·pér·bo·la› {{《}}▍ s.f.{{》}} {{♂}}En geometría,{{♀}} curva plana y simétrica que resulta de cortar una superficie cónica por un plano paralelo a su eje: • El enunciado del problema pedía que… …   Diccionario de uso del español actual con sinónimos y antónimos

  • hipêrbola — e ž (é) 1. geom. krivulja, katere točke imajo stalno razliko oddaljenosti od dveh danih točk: gorišče, os hiperbole / enakoosna hiperbola 2. lit. besedna figura, ki izraža pretiravanje: silnost pesnikovega čustva je ponazorjena s hiperbolo …   Slovar slovenskega knjižnega jezika

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”