- Horno cuerpo negro
-
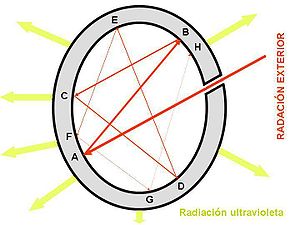
La mayoría de los cuerpos negros utilizados en experimentos de laboratorio se denomina "Horno cuerpo negro", que consiste en una cavidad con una abertura muy pequeña para que desde el exterior ingrese la radiación incidente. La radiación exterior, ingresa al horno a través del agujero, y en su interior choca contra la pared interior del horno que en parte es absorbida y en parte reflejada. Luego la porción reflejada choca con otro punto de la pared interior, la cual absorbe otra porción y la refleja parcialmente, y así continúa el ciclo. Pasado cierto tiempo y luego de sucesivas reflexiones, la radiación exterior incidente es totalmente absorbida.
En donde A, B, C, D, E, F, G y H son nodos en la pared interior de la cavidad del "Horno cuerpo negro".
La pared exterior del horno, generan un espectro de radiación desde el interior de la cavidad llamado "radiación de cavidad". Por consiguiente, la radiación del interior de una cavidad cuyas paredes están a una temperatura
 es de la misma índole que la radiación emitida por la superficie de un cuerpo negro a temperatura
es de la misma índole que la radiación emitida por la superficie de un cuerpo negro a temperatura  .
.El color (cromaticidad) corresponde a la radiación que depende de la temperatura del cuerpo negro; ese espacio es conocido como el "locus Planckian".
Lord Rayleig y sir James Jeans demostraron que la radiación dentro de cada cavidad de volumen
 consta de ondas estacionarias con nodos en las paredes. Calcularon el número de ondas estacionarias para el intervalo de frecuencia
consta de ondas estacionarias con nodos en las paredes. Calcularon el número de ondas estacionarias para el intervalo de frecuencia  a
a  como:
como:
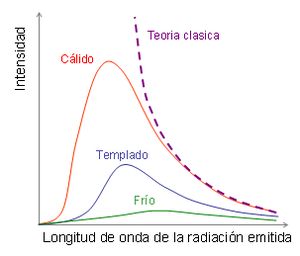
Para un radiador de , cuando la frecuencia se reduce a cero , el espectro predicho por la fórmula clásica de Rayleigh y Jeans se acerca más y más al espectro observado experimentalmente. Sin embargo, cuando la frecuencia se aumenta a valores de la región ultravioleta del espectro, el resultado teórico clásico difiere enormemente del experimento, ya que la “formula matemática” predice una densidad de energía infinita, cuando la densidad de la energía, a frecuencias muy altas, tiende a cero, lo que se llamó catástrofe ultravioleta.
, cuando la frecuencia se reduce a cero , el espectro predicho por la fórmula clásica de Rayleigh y Jeans se acerca más y más al espectro observado experimentalmente. Sin embargo, cuando la frecuencia se aumenta a valores de la región ultravioleta del espectro, el resultado teórico clásico difiere enormemente del experimento, ya que la “formula matemática” predice una densidad de energía infinita, cuando la densidad de la energía, a frecuencias muy altas, tiende a cero, lo que se llamó catástrofe ultravioleta.Contenido
Energía
En la Física clásica el nivel de energía puede tener cualquier valor en una gama continua que parte desde cero hasta llegar a grandes magnitudes. Sin embargo, para Planck ello no es así, ya que en vez de ser valores continuos se tratan de valores Discreto como sucede en:

Así como en el conjunto de los números naturales corresponde a un conjunto discreto, también lo es la energía de los estados cuánticos:
-
-
 es la Constante de Planck
es la Constante de Planck
-
No parece que los péndulos tengan energía discreta como lo postula Planck, sino que a la inversa, dan la impresión de que en su recorrido indefectiblemente viajan a través de una gama continuo de energía, a medida que sigue su movimiento oscilante. Algunas personas, podrán argüir que para oscilaciones, dentro de nuestro marco cotidiano, no es visible ni es detectable la naturaleza “cuantizada” del recorrido de péndulo en oscilación. Y agregaran, que los sistemas macroscópicos no revelaran si el postulado de Planck es válido o no.Gráfica de la fórmula clásica
La curva punteada (en violeta) grafica la fórmula clásica de Rayleigh y Jeans, que tiende al infinito. En donde la caparazón del Horno, debiera radiar una energía que tendiera al infinito, que, en el hecho, no se observa. En efecto, a medida que la temperatura disminuye, el pico del cuerpo negro de la curva de la radiación se mueve a menor intensidad y longitudes de onda más largas. En consecuencia la radiación gráficada del cuerpo negro es comparación con el modelo clásico de Rayleigh y Jeans.
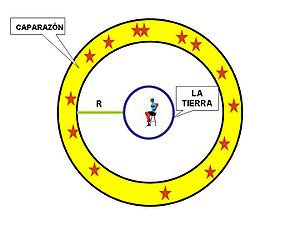
La situación anterior, es muy semejante a la Paradoja de Olbers en donde se suponía que la energía iría en aumento hasta llegar a un flujo luminoso igual a 50.000 veces la luz del Sol, cuanto está en cenit, con una temperatura de 10.000º Fahrenheit, que todo lo calcinaría.
Olbers, consideró que existía una caparazón que contenía las estrellas, la cual le asignó los siguientes valores:- Al radio lo llamó

- Al espesor de la caparzón

- La superfiecie de la esfera sobre la cual está construida la caparazón es

- Luego el volumen de la caparazón será

- El número de estrellas será

- Si el promedio de la luz emitida por una estrella individual es
 , entonces todas las estrellas emiten
, entonces todas las estrellas emiten 
Pero, lo que interesa no es cuanta luz emiten las estrellas, sino cuánta luz recibimos de ellas:
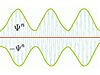
Sin embargo, este razonamiento no concuerda con la realidad, pues, según Olbers, debiéramos recibir un flujo luminoso que, en el hecho, no se observa.Suma de dos ondas con fasores
En la Física clásica, si hablando de ondas electromagnéticas, ellas son susceptibles de sufrir una perturbación ondulatoria, la que podemos representarla a través de una ecuación de forma:
Si a la ecuación de Lord Rayleig y sir James Jeans, se agrega la variante perturbación ondulatoria, acontecerá que la curva no tenderá al infinito, sino que será más parecida a la gráfica que presenta la física cuántica, dado que dos ondas electromagnéticas fuera de fase, en los casos en que
 , tiende a cero, la que se puede descomponer nuevamente en dos ondas separadas utilizando un diodo electrónico.
, tiende a cero, la que se puede descomponer nuevamente en dos ondas separadas utilizando un diodo electrónico.Se puede representar a
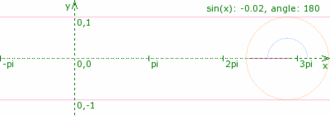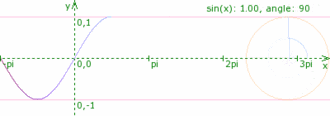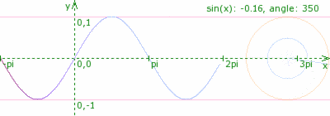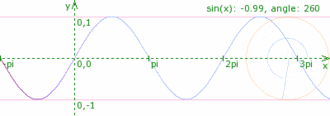
 por un vector giratorio (fasor). El fasor de magnitud
por un vector giratorio (fasor). El fasor de magnitud  formará un ángulo
formará un ángulo  . A medida que aumenta que trascurra el tiempo,
. A medida que aumenta que trascurra el tiempo,  se incrementa y la “punta” del fasor
se incrementa y la “punta” del fasor  es «cocíclico» pues gira en torno al perímetro del círculo con velocidad angular
es «cocíclico» pues gira en torno al perímetro del círculo con velocidad angular  . A medida que el fasor
. A medida que el fasor  gira,
gira,  representa la magnitud de la perturbación ondulatoria en cualquier tiempo.
representa la magnitud de la perturbación ondulatoria en cualquier tiempo.
Para este caso, tanto el fasor de como el
como el  , tienen una magnitud equivalente al radio del semicírculo (color rojo) dibujado por el cicloide:
, tienen una magnitud equivalente al radio del semicírculo (color rojo) dibujado por el cicloide:- De allí que

 , sea igual al diámetro del semicírculo descrito por el cicloide.
, sea igual al diámetro del semicírculo descrito por el cicloide.
- Y que

 , sea cero.
, sea cero.






Nº Variable = 
Variable = 
1 


2 


3 


4 


5 


6 


7 


8 


9 


Cuando es máximo, es que
es máximo, es que  es
es 
En tanto
 cuando
cuando 
Análisis de la onda radial
Las líneas, tanto magnéticas como electromagnéticas, tienen la propiedad de repelerse cuando entre ellas tienen sentido contrario, ya que en general ellas no se cortar, no se traslapan, ni se cruzan. En la transmisiones radiales se utiliza aquella propiedad.
La corriente alterna, al viajar por la antena transmisora, en el semiciclo positivo generando un campo magnética en el sentido que giran las manecillas del reloj, como lo señala la ley de la mano derecha; pero cuando la electricidad en la antena, viaja en su semiciclo negativo (sentido contrario al semiciclo anterior), las ondas magnéticas del campo también giran en el sentido contrario (ver Onda periódica).
En el instante que la corriente deja de circular en la antena, para cambiar de sentido, el campo electromagnético se contrae. Si la oscilación es de una frecuencia
 suficiente, el campo, no logrará contraerse totalmente, antes que llegue la corriente en sentido inverso, generando al interior del campo anterior, un nuevo campo también inverso que se expande. Con altas frecuencia
suficiente, el campo, no logrará contraerse totalmente, antes que llegue la corriente en sentido inverso, generando al interior del campo anterior, un nuevo campo también inverso que se expande. Con altas frecuencia  , las sucesivas y rápidas expansiones y contracciones del campo, genera que aquellos se alejen de la antena. Así se genera las ondas radiales.
, las sucesivas y rápidas expansiones y contracciones del campo, genera que aquellos se alejen de la antena. Así se genera las ondas radiales.El largo de la antena es
 , la cual, por muy pequeña que sea, tiene que tener alguna magnitud:
, la cual, por muy pequeña que sea, tiene que tener alguna magnitud:  . El largo
. El largo  de la antena, corresponde de una variable que depende de la frecuencia
de la antena, corresponde de una variable que depende de la frecuencia  . Un semiciclo, de la frecuencia
. Un semiciclo, de la frecuencia  , requiere del tiempo
, requiere del tiempo  para recorrer el largo
para recorrer el largo  .
.En el caso de una antena que emite con polarización vertical (campo eléctrico vertical) el cálculo del campo eléctrico resultante es el mismo que en radiación de un par de antenas. El resultado es:
La inversión de signo para el campo paralelo solo cambia un coseno en un seno:
En estas dos fórmulas:
 es el campo eléctrico de la onda electromagnética radiado por la antena si no hubiese la tierra.
es el campo eléctrico de la onda electromagnética radiado por la antena si no hubiese la tierra. es el número de onda.
es el número de onda. es la longitud de onda.
es la longitud de onda. es el largo de la antena.
es el largo de la antena.
La presencia y la magnitud, tanto del largo
 como del tiempo
como del tiempo  , impide que por lo general la perturbación ondulatoria lleve a la amplitud de onda de la onda radial a un valor igual o inferior a cero, para el evento que se trate de una transmisión por Amplitud Modulada.
, impide que por lo general la perturbación ondulatoria lleve a la amplitud de onda de la onda radial a un valor igual o inferior a cero, para el evento que se trate de una transmisión por Amplitud Modulada.Al considerar la señal moduladora (señal del mensaje) como:
y Señal portadora como:
La ecuación de la señal modulada en AM es la siguiente:
- y(t) = Señal modulada
- xn(t) = Señal moduladora normalizada con respecto a su amplitud = ys(t) / As
- m = Índice de modulación (suele ser menor que la unidad)=As / Ap
Lo señalado denota que en este caso de "Ondas radiales" no es aplicable las fórmulas para el caso de dos fasores, en donde se sostuvo que:
Cuando es máximo, es que
es máximo, es que  es
es 
En tanto
 cuando
cuando 
Historia
Planck, en un principio cuantizó exclusivamente la energía de los electrones de las paredes de la cavidad, pues no aceptó la idea de que las ondas electromagnéticas oscilantes del interior de la cavidad del horno también estuvieran cuantizadas, y durante diez años trato de unificar la idea cuántica con la teoría clásica, resistiendo las ideas sobre la teoría cuántica de la radiación electromagnética elaborada por Einstein.
-
Wikimedia foundation. 2010.














![y(t) ={ A_p}\cdot[{1+{m\cdot x_n(t)}}]\cdot cos(w_p \cdot t)](e/29ebf4dfcc23384aecc0cac92004c664.png)
