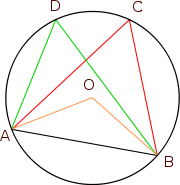
- Puntos cocíclicos
-
Puntos cocíclicos
Los puntos cocíclicos son aquellos que pertenecen a una misma circunferencia.
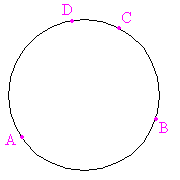
Dos puntos siempre son cocíclicos (caso trivial). Tres puntos siempre serán cocíclicos excepto en el caso de que estén alineados.
Cuando cuatro puntos son cocíclicos forman un cuadrilátero cíclico, y tales cuadriláteros tienen muchas propiedades notables.
Propiedades de puntos cocíclicos
Un segmento cuyos extremos estén en una circunferencia se llama cuerda de éste.
Si <ABC> es el ángulo algebraico entre los vectores BA y BC.
Teorema 1: Ángulo al centro
Sean A, B y C tres puntos cocíclicos, y O el centro del círculo que pasa por A, B y C (O es el circuncentro, o centro del círculo circunscrito al triángulo). Entonces, si C y O están del mismo lado de la cuerda AB, el ángulo <AOB> es el doble del ángulo <ACB>.
Si C cruza la cuerda, su ángulo se cambia por su suplementario.
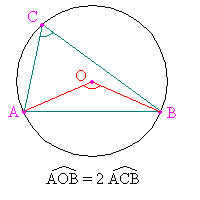
Prueba:
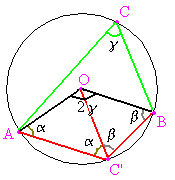
Al completar la figura con el segmento [OC] se obtiene tres triángulos isósceles: AOB, AOC y BOC, porque OA = OB = OC (radio del círculo). Considerando ABC, se da la igualdad 2α + 2β + 2γ = π (radios).
<ACB> = α + β por una parte, y por otra parte: <AOB> = π - 2γ (triángulo AOB) = 2α + 2β (triángulo ABC) = 2(α + β ) = 2 <ACB>.
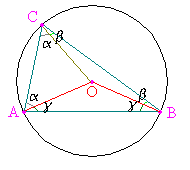
En el segundo caso, <AC'B> = α + β, y 2α + 2β + 2γ = 2π (en el cuadrilátero OAC'B) lo que da al dividir por 2: <AC'B> = π - γ que es el suplementario de <ACB> = γ.
Primera consecuencia:
Teorema 2:
En un cuadrilátero inscrito en un círculo, los ángulos opuestos son suplementarios.
Basta con tomar las diagonales como cuerdas, y aplicar el teorema precedente.
Segunda consecuencia:
Teorema 3: Ángulo constante
Sean A, B, C y D cuatro puntos cocíclicos, colocados en este orden en el círculo. Entonces tenemos la igualdad de ángulos: <ACB> = <ADB>
Prueba: Ambos ángulos miden el doble del ángulo al centro <AOB>.Dicho de otro modo, si se considera la cuerda [AB], y un punto móvil que recorre el círculo quedándose del mismo lado con relación a [AB], entonces el ángulo <AMB> es constante. Se dice que se ve [AB] desde M bajo un ángulo constante. Tomando otra cuerda, se obtiene otra igualdad: por ejemplo, con [BC]: <BAC> = <BDC>.
Una aplicación de todos estos teoremas se encuentra en la demostración relativa a la recta de Simson.
- El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.
Categoría: Geometría
Wikimedia foundation. 2010.