Módulo de cizalladura

Módulo de cizalladura

El módulo de cizalladura, también llamado módulo de elasticidad transversal, es una constante elástica que caracteriza el cambio de forma que experimenta un material elástico (lineal e isótropo) cuando se aplican esfuerzos cortantes. Este módulo recibe una gran variedad de nombres, entre los que cabe destacar los siguientes: Módulo de rigidez transversal, módulo de corte, módulo de cortadura, módulo elástico tangencial, módulo de elasticidad transversal.

Para un material elástico lineal e isótropo, el módulo de elasticidad transversal tiene el mismo valor para todas las direcciones del espacio. En materiales anisótropos se pueden definir varios módulos de de elasticidad transversal, y en los materiales elásticos no lineales dicho módulo no es una constante sino que es una función dependiente del grado de deformación.

Contenido

Definición

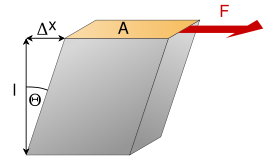
fig. 1 Esquema para la medición del esfuerzo cortante.

Experimentalmente el módulo elástico transversal (o módulo cortitilatante) puede medirse de varios modos, conceptualmente la forma más sencilla es considerar un cubo como el de la fig. 1 y someterlo a una fuerza cortante, para pequeñas deformaciones se puede calcular la razón entre la tensión y la distorsión angular:


G := \frac{\tau_m}{\Theta} \approx \frac{F/A}{\Delta x/h} = \frac{F h}{\Delta x A}

Materiales isótropos lineales

Para un material isótropo elástico lineal el módulo de elasticidad transversal está relacionado con el módulo de Young y el coeficiente de Poisson mediante la relación:

G = \frac{E}{2(1+\nu)} = \frac{\tau_{ij}}{2\varepsilon_{ij}}


Donde:

E \, es el módulo de elasticidad longitudinal o módulo de Young.
\nu \, es el coeficiente de Poisson.
τij,εij son respectivamente la tensión tangencial y la deformación tangencial sobre el plano formado por los ejes Xi y Xj.

Materiales anisótropos

Los materiales elásticos lineales anisótropos se caracterizan por presentar diferentes valores de las constantes elásticas según la dirección en la que se aplican las fuerzas. En general, en un material anisótropo al aplicar esfuerzos tangentes a una superficie aparecen deformaciones normales a ésta. Eso significa que los modos transversales y longitudinales no están desacoplados y por esa razón los conceptos de módulo de elasticidad longitudinal y módulo de elasticidad transversal no se pueden generalizar adecuadamente, en todos los casos.

Materiales ortótropos

Un caso particular de material anisótropo donde sí se puede hablar de módulos de elasticidad longitudinales y transversales son los llamados materiales ortótropos; la madera es un ejemplo de material ortótropo, frecuentemente usado en construcción. En los materiales ortótropos los modos transversales y longitudinales de deformación están desacoplados. Eso permite identificar claramente módulos de elasticidad transversal y módulos de elasticidad longitudinal. Para un material ortótropo general pueden definirse tres módulos de elasticidad longitudinales básicos (Ex, Ey', Ez) y tres módulos de elasticidad transversal (Gxy, Gxz', Gyz). Estos últimos se definen como:

G_{xy} = \frac{\sigma_{xy}}{2\varepsilon_{xy}} \qquad G_{xz} = \frac{\sigma_{xz}}{2\varepsilon_{xz}} \qquad G_{yz} = \frac{\sigma_{yz}}{2\varepsilon_{yz}}


Para un material como la madera las coordenadas X, Y y Z anteriores se toman de la siguiente manera:

  • el eje X está alineado con la dirección longitudinal de la fibra.
  • el eje Y se toma perpendicular a los anillos de la sección transversal.
  • el eje Z se toma tangente a los anillos de la sección transversal.

Los módulos de elasticidad transversal en estas tres direcciones son diferentes para la madera y pueden llegar a presentar grandes diferencias de valor entre ellas.

Valores para varios materiales

Para ver el valor del módulo de elasticidad transversal para varios materiales consultar los valores del módulo de elasticidad transversal del Anexo:Constantes elásticas de diferentes materiales.

Véase también

Módulos de elasticidad para materiales homogeneos isótropos
Módulo de compresibilidad (K) • Módulo de Young (E) • Primer parámetro de Lamé (λ) • Módulo de cizalladura (G) • Coeficiente de Poisson (ν) • Módulo de onda P (M)
Fórmulas de conversión
Los materiales elásticos lineales isótropos homogéneos tienen sus propiedades elásticas únicamente determinadas por dos módulos cualesquiera de los especificados anteriormente, por lo tanto, cualquier otro módulo de elasticidad puede ser calculado de acuerdo a estas fórmulas.
(\lambda,\,G) (E,\,G) (K,\,\lambda) (K,\,G) (\lambda,\,\nu) (G,\,\nu) (E,\,\nu) (K,\, \nu) (K,\,E) (M,\,G)
K=\, \lambda+ \frac{2G}{3} \frac{EG}{3(3G-E)} \lambda\frac{1+\nu}{3\nu} \frac{2G(1+\nu)}{3(1-2\nu)} \frac{E}{3(1-2\nu)} M - \frac{4G}{3}
E=\, G\frac{3\lambda + 2G}{\lambda + G} 9K\frac{K-\lambda}{3K-\lambda} \frac{9KG}{3K+G} \frac{\lambda(1+\nu)(1-2\nu)}{\nu} 2G(1+\nu)\, 3K(1-2\nu)\, G\frac{3M-4G}{M-G}
\lambda=\, G\frac{E-2G}{3G-E} K-\frac{2G}{3} \frac{2 G \nu}{1-2\nu} \frac{E\nu}{(1+\nu)(1-2\nu)} \frac{3K\nu}{1+\nu} \frac{3K(3K-E)}{9K-E} M - 2G\,
G=\, 3\frac{K-\lambda}{2} \lambda\frac{1-2\nu}{2\nu} \frac{E}{2(1+\nu)} 3K\frac{1-2\nu}{2(1+\nu)} \frac{3KE}{9K-E}
\nu=\, \frac{\lambda}{2(\lambda + G)} \frac{E}{2G}-1 \frac{\lambda}{3K-\lambda} \frac{3K-2G}{2(3K+G)} \frac{3K-E}{6K} \frac{M - 2G}{2M - 2G}
M=\, \lambda+2G\, G\frac{4G-E}{3G-E} 3K-2\lambda\, K+\frac{4G}{3} \lambda \frac{1-\nu}{\nu} G\frac{2-2\nu}{1-2\nu} E\frac{1-\nu}{(1+\nu)(1-2\nu)} 3K\frac{1-\nu}{1+\nu} 3K\frac{3K+E}{9K-E}

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • cizalladura — cizalladura. f. Mec. Deformación producida en un sólido por la acción de dos fuerzas opuestas, iguales y paralelas. * * * ► femenino MECÁNICA Deformación en la que solo intervienen fuerzas tangenciales. Es un corrimiento de las superficies donde… …   Enciclopedia Universal

  • Módulo de Young — Diagrama tensión deformación. El módulo de Young viene representado por la tangente a la curva en cada punto. Para materiales como el acero resulta aproximadamente constante dentro del límite elástico. El módulo de Young o módulo elástico… …   Wikipedia Español

  • Módulo — El término módulo (del latín modŭlus) puede referirse a: una dimensión que convencionalmente se toma como unidad de medida: en arquitectura, el módulo es la medida que se toma como base para dimensionar todo el edificio Módulo vitruviano Modulor… …   Wikipedia Español

  • Módulo de compresibilidad — Ilustración de compresión uniforme. El módulo de compresibilidad ( ) de un material mide su resistencia a la compresión uniforme y, por tanto, indica el aumento de presión requerido para causar una disminución unitaria de volumen dada. El módulo… …   Wikipedia Español

  • Módulo elástico — Un modulo elástico es un tipo de constante elástica que relaciona una medida relacionada con la tensión y una medida relacionada con la deformación. Los materiales elásticos isótropos quedan caraterizados por un módulo elástico y un coeficiente… …   Wikipedia Español

  • Módulo de rigidez — El modulo de rigidez puede referirse a: Módulo de rigidez constante elástica a veces llamado impropiamente módulo de cizalladura. Constantes de rigidez de un elemento que caracterizan su deformabilidad en función de su geometría y su material.… …   Wikipedia Español

  • Parámetros de Lamé — Saltar a navegación, búsqueda En elasticidad lineal, los parámetros de Lamé son los siguientes dos parámetros λ, también conocido como primer parámetro de Lamé. μ, el módulo de elasticidad transversal o segundo parámetro del Lamé. los cuales en… …   Wikipedia Español

  • Coeficiente de Poisson — Ensanchamiento por efecto Poisson del plano longitudinal medio de un prisma comprimido a lo largo de su eje, el grado de ensanchamiento depende del coeficiente de Poisson, en este caso se ha usado El coeficiente de Poisson (denotado mediante la… …   Wikipedia Español

  • Cesio — «cs» redirige aquí. Para otras acepciones, véase CS. Xenón ← Cesio → Bario Rb …   Wikipedia Español

  • Osmio — Renio ← Osmio → Iridio Ru   …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”