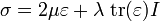Parámetros de Lamé

En elasticidad lineal, los parámetros de Lamé son los siguientes dos parámetros

λ, también conocido como primer parámetro de Lamé.
μ, el módulo de elasticidad transversal o segundo parámetro del Lamé.

los cuales en materiales homogéneos e isótropos satisfacen la ley de Hooke en 3D,

$\sigma=2\mu \varepsilon +\lambda \; \mathrm{tr}(\varepsilon)I$

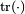donde σ es la tensión, ε el tensor de deformación, la $\scriptstyle I$ la matriz identidad y $\scriptstyle\mathrm{tr}(\cdot)$ la función traza.

El primer parámetro λ no tiene una interpretación física, pero sirve para simplificar la matriz de rigidez en la ley de Hooke. Los dos parámetrs juntos constituyen una parametrización del módulo de elasticidad para el medio isótropo homogéneo, y están así relacionadas con el otro módulo de elasticidad.

Los parámetros son nombrados después por Gabriel Lamé.

Referencias

F. Kang, S. Zhong-Ci, Mathematical Theory of Elastic Structures, Springer New York, ISBN 0-387-51326-4, (1981)
G. Mavko, T. Mukerji, J. Dvorkin, The Rock Physics Handbook, Cambridge University Press (paperback), ISBN 0-521-54344-4, (2003)

Módulos de elasticidad para materiales homogeneos isótropos
Módulo de compresibilidad ( $K$ ) • Módulo de Young ( $E$ ) • Primer parámetro de Lamé ( $λ$ ) • Módulo de cizalladura ( $G$ ) • Coeficiente de Poisson ( $ν$ ) • Módulo de onda P ( $M$ )

Fórmulas de conversión
Los materiales elásticos lineales isótropos homogéneos tienen sus propiedades elásticas únicamente determinadas por dos módulos cualesquiera de los especificados anteriormente, por lo tanto, cualquier otro módulo de elasticidad puede ser calculado de acuerdo a estas fórmulas.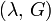
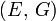
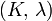
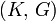
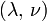
	$(\lambda,\,G)$	$(E,\,G)$	$(K,\,\lambda)$	$(K,\,G)$	$(\lambda,\,\nu)$	$(G,\,\nu)$	$(E,\,\nu)$	$(K,\, \nu)$	$(K,\,E)$	$(M,\,G)$
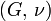
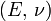
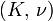
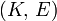
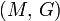
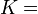
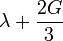
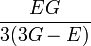
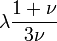
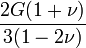
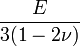
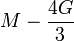
$K=\,$	$\lambda+ \frac{2G}{3}$	$\frac{EG}{3(3G-E)}$			$\lambda\frac{1+\nu}{3\nu}$	$\frac{2G(1+\nu)}{3(1-2\nu)}$	$\frac{E}{3(1-2\nu)}$			$M - \frac{4G}{3}$
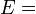
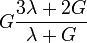
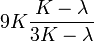
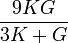
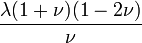
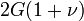
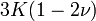
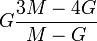
$E=\,$	$G\frac{3\lambda + 2G}{\lambda + G}$		$9K\frac{K-\lambda}{3K-\lambda}$	$\frac{9KG}{3K+G}$	$\frac{\lambda(1+\nu)(1-2\nu)}{\nu}$	$2G(1+\nu)\,$		$3K(1-2\nu)\,$		$G\frac{3M-4G}{M-G}$
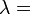
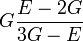
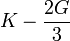
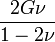
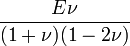
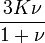
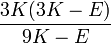
$\lambda=\,$		$G\frac{E-2G}{3G-E}$		$K-\frac{2G}{3}$		$\frac{2 G \nu}{1-2\nu}$	$\frac{E\nu}{(1+\nu)(1-2\nu)}$	$\frac{3K\nu}{1+\nu}$	$\frac{3K(3K-E)}{9K-E}$	$M - 2G\,$
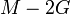
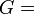
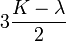
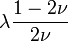
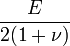
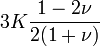
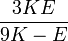
$G=\,$			$3\frac{K-\lambda}{2}$		$\lambda\frac{1-2\nu}{2\nu}$		$\frac{E}{2(1+\nu)}$	$3K\frac{1-2\nu}{2(1+\nu)}$	$\frac{3KE}{9K-E}$
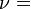
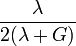
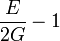
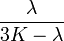
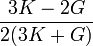
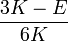
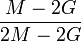
$\nu=\,$	$\frac{\lambda}{2(\lambda + G)}$	$\frac{E}{2G}-1$	$\frac{\lambda}{3K-\lambda}$	$\frac{3K-2G}{2(3K+G)}$					$\frac{3K-E}{6K}$	$\frac{M - 2G}{2M - 2G}$
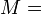
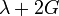
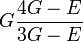
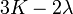
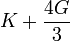
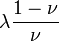
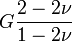
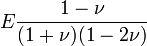
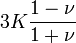
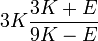$M=\,$	$\lambda+2G\,$	$G\frac{4G-E}{3G-E}$	$3K-2\lambda\,$	$K+\frac{4G}{3}$	$\lambda \frac{1-\nu}{\nu}$	$G\frac{2-2\nu}{1-2\nu}$	$E\frac{1-\nu}{(1+\nu)(1-2\nu)}$	$3K\frac{1-\nu}{1+\nu}$	$3K\frac{3K+E}{9K-E}$

Obtenido de "Par%C3%A1metros de Lam%C3%A9"

Categorías: Mecánica de medios continuos | Resistencia de materiales | Ingeniería estructural

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

LAME (codificador) — LAME Desarrollador The LAME development team … Wikipedia Español
Ecuación de onda — Saltar a navegación, búsqueda La ecuación de onda es una importante ecuación diferencial parcial lineal de segundo orden que describe la propagación de una variedad de ondas, como las ondas sonoras, las ondas de luz y las ondas en el agua. Es… … Wikipedia Español
Constante elástica — Una constante elástica es cada uno de los parámetros físicamente medibles que caracterizan el comportamiento elástico de un sólido deformable elástico. A veces se usa el término constante elástica también para referirse a los coeficientes de… … Wikipedia Español
Mecánica de sólidos deformables — La mecánica de los sólidos deformables estudia el comportamiento de los cuerpos sólidos deformables ante diferentes tipos de situaciones como la aplicación de cargas o efectos térmicos. Estos comportamientos, más complejos que el de los sólidos… … Wikipedia Español
Resistencia de materiales — Saltar a navegación, búsqueda Para otros usos de este término, véase Resistencia. La resistencia de materiales clásica es una disciplina de la ingeniería mecánica y la ingeniería estructural que estudia los sólidos deformables mediante modelos… … Wikipedia Español
Ibagué — Bandera … Wikipedia Español
MediaCoder — Desarrollador Stanley Huang www.mediacoderhq.com … Wikipedia Español
Onda elástica — Una onda elástica es una perturbación tensional que se propaga a lo largo de un medio elástico. Por ejemplo las ondas sísmicas ocasionan temblores que pueden tratarse como ondas elásticas que se propagan por el terreno. Contenido 1 Ecuación de… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Parámetros de Lamé

Parámetros de Lamé

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Parámetros de Lamé

Parámetros de Lamé

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo