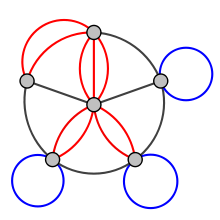
Multigrafo

Multigrafo
Un multigrafo con múltiples aristas (en rojo) y tres bucles (en azul). No todos los autores permiten multigrafos con bucles.

Un multigrafo o pseudografo es un grafo que está facultado para tener aristas múltiples; es decir, aristas que relacionan los mismos nodos. De esta forma, dos nodos pueden estar conectados por más de una arista. Formalmente, un multigrafo G es un par ordenado G:=(V, E) donde:

  • V es un conjunto de vértices o nodos
  • E es un multiconjunto de pares no ordenados de nodos, llamados aristas o líneas.

Ejemplo. Los multigrafos podrían usarse, por ejemplo, para modelar las posibles conexiones de vuelo ofrecidas por una aerolínea. Para este caso tendríamos un grafo dirigido, donde cada nodo es una localidad y donde pares de aristas paralelas conectan estas localidades, según un vuelo es hacia o desde una localidad a la otra.

Algunos autores permiten que los multigrafos tengan bucles, es decir, que una arista conecte a un nodo consigo mismo.[1]

Un multidigrafo es un grafo dirigido que está facultado para tener aristas múltiples, es decir, aristas con los mismos nodos iniciales y finales. Formalmente, un multidigrafo G es un par ordenado G:=(V,A) donde:

  • V es un conjunto de vértices o nodos
  • A es un multiconjunto de pares ordenados de nodos, llamados aristas dirigidas, arcos o flechas.

Un multidigrafo mixto G:=(V,E,A) puede definirse de la misma manera que un grafo mixto, es decir, con la capacidad de poseer al mismo tiempo aristas dirigidas (A) y no dirigidas (E).

Etiquetado

Los multigrafos y multidigrafos pueden etiquetarse de manera análoga a un grafo tradicional. Sin embargo, sólo existe consenso con respecto a la terminología para los multidigrafos.

Un multidigrafo etiquetado G es un grafo etiquetado con arcos etiquetados. Formalmente, es una 8-tupla G=(\Sigma_V, \Sigma_A, V, A, s, t, \ell_V, \ell_A) donde:

  • V es un conjunto de nodos y A un multiconjunto de arcos.
  • ΣV y ΣA son alfabetos finitos para las etiquetas de nodos y arcos.
  • s\colon A\rightarrow\ V y t\colon A\rightarrow\ V son dos funciones que indican la fuente y objetivo de los nodos de un arco.
  • \ell_V\colon V\rightarrow\Sigma_V y \ell_A\colon A\rightarrow\Sigma_A son dos funciones que asocian cada nodo y arco con una etiqueta.

Notas

  1. ↑ Por ejemplo, ver, Bollobas, p. 7 y Diestel, p. 25.

Referencias

  • Balakrishnan, V. K.; Graph Theory, McGraw-Hill; 1 edition (February 1, 1997). ISBN 0-07-005489-4.
  • Bollobas, Bela; Modern Graph Theory, Springer; 1st edition (August 12, 2002). ISBN 0-387-98488-7.
  • Diestel, Reinhard; Graph Theory, Springer; 2nd edition (February 18, 2000). ISBN 0-387-98976-5.
  • Gross, Jonathan L, and Yellen, Jay; Graph Theory and Its Applications, CRC Press (December 30, 1998). ISBN 0-8493-3982-0.
  • Gross, Jonathan L, and Yellen, Jay; (eds); Handbook of Graph Theory. CRC (December 29, 2003). ISBN 1-58488-090-2.
  • Harary, Frank; Graph Theory, Addison Wesley Publishing Company (January 1995). ISBN 0-201-41033-8.
  • Zwillinger, Daniel; CRC Standard Mathematical Tables and Formulae, Chapman & Hall/CRC; 31st edition (November 27, 2002). ISBN 1-58488-291-3.
  • Svante Janson, Donald E. Knuth, Tomasz Luczak, and Boris Pittel; The Birth of the Giant Component, Random Structures Algorithms 4 (1993), no. 3, 231-358.

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • multígrafo — sustantivo masculino 1. Origen: Venezuela. Multicopista …   Diccionario Salamanca de la Lengua Española

  • multígrafo — (De multi y ‒grafo). adj. Méx. y Ven. multicopista. U. m. c. s. m.) …   Diccionario de la lengua española

  • multígrafo — ► adjetivo/ sustantivo masculino México, Venezuela ARTES GRÁFICAS,TECNOLOGÍA Máquina para reproducir textos, dibujos, grabados, y otras cosas sobre papel. * * * multígrafo. (De multi y ‒grafo). adj. Méx. y …   Enciclopedia Universal

  • Aristas múltiples — Cuando un grafo admite aristas múltiples, se llama multigrafo. En teoría de grafos, las aristas múltiples (también llamadas aristas paralelas o una multi arista), son dos o más aristas que son incidentes (es decir, que conectan) a al menos dos… …   Wikipedia Español

  • Árbol de expansión — Un árbol de expansión (aristas azules gruesas) de un grafo de rejilla. En el campo matemático de la teoría de grafos, un árbol de expansión T de un grafo conexo, no dirigido G es un árbol compuesto por todos los vértices y algunas (quizá todas)… …   Wikipedia Español

  • Grafo — Para otros usos de este término, véase Grafo (desambiguación). Para la teoría en torno a este objeto matemático, véase Teoría de grafos. Grafo etiquetado con 6 vértices y 7 aristas. En matemáticas y ciencias de la computación, un grafo (del …   Wikipedia Español

  • Teoría de grafos — Diagrama de un grafo con 6 vértices y 7 aristas. En matemáticas y en ciencias de la computación, la teoría de grafos (también llamada teoría de las gráficas) estudia las propiedades de los grafos (también llamadas gráficas). Un grafo es un… …   Wikipedia Español

  • Bucle (teoría de grafos) — Un grafo con un bucle en el vértice 1. En teoría de grafos, un bucle o loop es una arista que conecta un vértice consigo mismo. Un grafo simple no posee bucles. Dependiendo del contexto, un grafo o multigrafo puede estar definido o no para… …   Wikipedia Español

  • Francisco José Delgado (Venezuela) — Francisco José Delgado Francisco José Delgado, mejor conocido como Kotepa Delgado, fue un político y periodista venezolano, co fundador del Partido Comunista de Venezuela Contenido 1 Biografía …   Wikipedia Español

  • Glosario en teoría de grafos — Anexo:Glosario en teoría de grafos Saltar a navegación, búsqueda Grafo con 6 nodos A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”