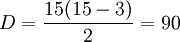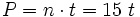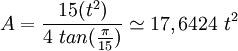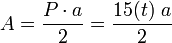Pentadecágono

Pentadecágono

Pentadecágono

Pentadecágono regular.

En geometría, un pentadecágono es un polígono de 15 lados y 15 vértices.

Propiedades

Un pentadecágono tiene 90 diagonales, resultado que se puede obtener aplicando la ecuación general para deteminar el número de diagonales de un polígono, D = n(n − 3) / 2; siendo el número de lados n = 15, tenemos:

D=\frac{15(15-3)}{2}=90

La suma de todos los ángulos internos de cualquier pentadecágono es 2340 grados ó 13π radianes.

Pentadecágono regular

Un pentadecágono regular es el que tiene todos sus lados de la misma longitud y todos sus ángulos internos iguales. Cada ángulo interno del pentadecágono regular mide 156º ó 13π / 15 rad. Cada ángulo externo del pentadecágono regular mide 24º ó 2π / 15 rad.

Al multiplicar la longitud t de un lado de un pentadecágono regular por quince (el número de lados n del polígono) obtendremos la longitud de su perímetro P.

P = n\cdot t = 15\ t

El área A de un pentadecágono regular de lado t es de la siguiente forma:

A = \frac{15(t^2)}{4\ tan(\frac{\pi}{15})}\simeq 17,6424\ t^2

donde π es la constante pi y tan es la función tangente calculada en radianes.

Si se conoce la longitud del apotema a del polígono, otra alternativa para calcular el área es:

A = \frac{P\cdot a}{2} = \frac{15(t)\ a}{2}

Enlaces externos

Commons

Obtenido de "Pentadec%C3%A1gono"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • pentadecágono — s. m. [Geometria] Polígono de quinze lados e quinze ângulos.   ‣ Etimologia: penta + decágono …   Dicionário da Língua Portuguesa

  • pentadecágono — pentadecágono, na adjetivo,sustantivo masculino 1. Área: geometría [Polígono] que tiene quince ángulos y quince lados …   Diccionario Salamanca de la Lengua Española

  • pentadecágono — (De penta y decágono). adj. Geom. Dicho de un polígono: De quince ángulos y quince lados. U. m. c. s. m.) …   Diccionario de la lengua española

  • pentadecágono — (Del gr. pente , cinco + deka, diez + gonia, ángulo.) ► adjetivo/ sustantivo masculino GEOMETRÍA Se aplica al polígono de quince ángulos y quince lados. TAMBIÉN pentedecágono * * * pentadecágono (de «penta » y «decágono») m. Geom. *Polígono de… …   Enciclopedia Universal

  • pentadecágono — {{＃}}{{LM P29771}}{{〓}} {{［}}pentadecágono{{］}}, {{［}}pentadecágona{{］}} ‹pen·ta·de·cá·go·no, na› {{《}}▍ adj./s.m.{{》}} {{♂}}En geometría, referido a un polígono,{{♀}} que tiene quince lados y quince ángulos. {{★}}{{＼}}ETIMOLOGÍA:{{／}} De penta… …   Diccionario de uso del español actual con sinónimos y antónimos

  • pentadecagono — pen·ta·de·cà·go·no s.m. TS geom. poligono con quindici lati e quindici angoli {{line}} {{/line}} DATA: 1821. ETIMO: comp. di pentadeca e 2 gono, cfr. gr. pentekaidekágōnon …   Dizionario italiano

  • pentadecagono — {{hw}}{{pentadecagono}}{{/hw}}s. m. Poligono con quindici lati …   Enciclopedia di italiano

  • pentadecagono — pl.m. pentadecagoni …   Dizionario dei sinonimi e contrari

  • Polígono — Saltar a navegación, búsqueda Un polígono es una figura geométrica conformada por segmentos consecutivos no alineados, llamados lados. Los polígonos cuyos lados no están en el mismo plano, se denominan polígonos alabeados. Existe la posibilidad… …   Wikipedia Español

  • Polígono — (Del gr. polys, numeroso + gonia, ángulo.) ► sustantivo masculino 1 GEOMETRÍA Porción de plano limitado por líneas rectas, cuyos segmentos se llaman lados. 2 Unidad urbanística constituida por una superficie de terreno delimitada como valoración… …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”