Esta propiedad que puede deducirse del principio de inducción es de particular importancia en matemática ya que se utiliza como base para la demostración por inducción.

• Principio de Buena Ordenación

Todo conjunto no vacío de enteros positivos contiene un elemento (un número entero) que es mínimo.

Nótese que esta propiedad es válida sólo para conjuntos cuyos elementos son números enteros positivos. No es cierta para cualquier conjunto, ya que si consideramos los enteros negativos, por ejemplo, no existe un menor elemento.

Demostración del Principio de Buena Ordenación

Como dijimos anteriormente, este principio se puede deducir a partir del principio de inducción. Usaremos entonces, este principio para demostrar el principio de buena ordenación.

Definamos un conjunto 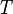tal que 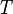es no vacío y consta sólo de enteros positivos. Queremos demostrar existe un 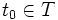tal que para para todo 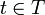, se tiene que .

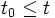Supongamos que no existe tal entero, y lleguemos a una contradicción. Es claro que 1 no puede pertenecer a 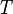, ya que de lo contrario éste sería su menor elemento. Designemos por 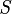al conjunto de todos los n tal que 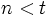, para todo 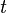de 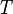. Entonces 1 pertenece a 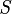, ya que 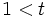. Sea 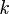un entero positivo de 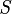. Entonces 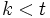para todo 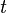de 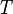. Demostraremos que 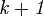también pertenece a 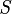. De no ser así, entonces para un cierto 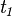de 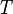tendríamos que 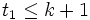. Puesto que 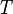no tiene menor elemento, existe u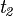n en 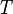tal que 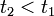, por lo tanto 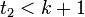. Esto implica que 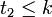, en contradicción con el hecho de que 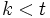para todo 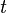de 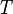. Por lo tanto podemos decir que 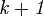pertenece a 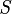. Luego, por el principio de inducción, concluímos que 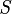contiene a todos los enteros positivos. Puesto que 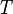es no vacío, existe un entero positivo 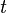en 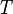. Pero este 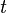debe pertenecer a 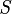ya que 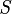los contiene a todos. Tenemos entonces que 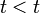, lo cual es una contradicción. Así entonces, nuestra hipótesis de que 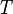no tiene un menor elemento es falsa. Luego 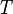posee un menor elemento.

Nótese que esto también demuestra que el principio de buena ordenación es una consecuencia del principio de inducción.