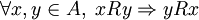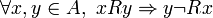Relación simétrica

Relación simétrica

Relación simétrica

Una relación binaria R sobre un conjunto A, es simétrica cuando se da que si un elemento está relacionado con otro mediante R, entonces ese otro también está relacionado con el primero.

Es decir,

\forall x,y\in A,\ xRy \Rightarrow yRx

En tal caso, decimos que R cumple con la propiedad de simetría.

La aplicación de cualquier relación R sobre un conjunto A, se representa con el par ordenado (A, R).

Cuando una relación es lo opuesto a una simétrica, es decir, cuando se da que si un elemento está relacionado con otro mediante R, entonces ese otro no está relacionado con el primero, entonces decimos que es asimétrica, lo que denotamos formalmente por:

\forall x,y\in A,\ xRy \Rightarrow y\neg Rx

En este caso, decimos que R cumple con la propiedad de asimetría.

Representación

Sea R una relación simétrica o asimétrica aplicada sobre un conjunto A, entonces R tiene una representación particular para cada forma de describir una relación binaria.

Notación Relación simétrica Relación asimétrica
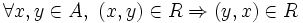
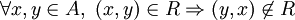
Como pares ordenados \forall x,y\in A,\ (x,y)\in R \Rightarrow (y,x)\in R \forall x,y\in A,\ (x,y)\in R \Rightarrow (y,x)\not\in R
Como matriz de adyacencia 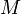M\,, la matriz transpuesta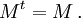 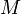M^t=M\,. M\,, tal matriz tiene una diagonal con sólo 0's, es decir, 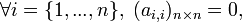\forall i=\{1, ..., n\}, \; (a_{i,i})_{n\times n}=0, y además 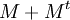M+M^t\, produce una matriz simétrica.
Como grafo Es un grafo que se puede representar como grafo no dirigido. Es un grafo dirigido sin bucles ni ciclos.

Ejemplos

Sea A un conjunto cualquiera:

  • Sea 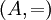(A, =)\,, =\, (la igualdad matemática), es simétrica.
  • Sea 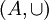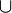(A, \cup), \cup es simétrica.
  • "Estar casado con" es una relación simétrica, mientras que "ser más alto que" no lo es.
  • Sea 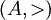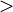(A, >)\,, >\, ("mayor estricto que") es asimétrica, al igual que 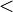<\, ("menor estricto que").
  • Sea 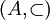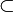(A, \subset), \subset (la inclusión estricta de conjuntos), es asimétrica.

Simetría 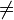\neq Antisimetría

La simetría no es lo opuesto de la antisimetría.

Existen relaciones que son simétricas y antisimétricas al mismo tiempo (como la igualdad), otras que no son simétricas ni antisimétricas (como la divisibilidad), otras que son simétricas pero no antisimétricas (como la relación de congruencia módulo n), y otras que son antisimétricas pero no simétricas (como la relación "menor que").

Obtenido de "Relaci%C3%B3n sim%C3%A9trica"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Relación simétrica — En matemáticas, una relación binaria R sobre un Conjunto X es simétrica si se cumple que para todo a y b pertenecientes a X, si a está relacionado con …   Enciclopedia Universal

  • Relación binaria — Saltar a navegación, búsqueda En matemáticas, una relación binaria es una relación matemática R entre los elementos de dos conjuntos A y B. Una relación de este tipo se puede representar mediante pares ordenados, : Las dos propo …   Wikipedia Español

  • Relación — Saltar a navegación, búsqueda El concepto relación puede referirse a muy distintos ámbitos: Contenido 1 En el sentido de relato 1.1 Folclore 1.2 Literatura …   Wikipedia Español

  • Relación total — Saltar a navegación, búsqueda Una relación binaria R sobre un conjunto A es una relación total cuando se cumple que para cada dos elementos a y b de A, ó a esta relacionado con b ó b esta relacionado con a, esto es: Tenga en cuenta que esto… …   Wikipedia Español

  • Relación transitiva — Ejemplo: Si a es mayor que b, y b es mayor que c, entonces, a es mayor que c. Una relación binaria R sobre un conjunto A es transitiva cuando se cumple: siempre que un elemento se relaciona con otro y éste último con un tercero, entonces el… …   Wikipedia Español

  • Relación bien fundada — En teoría de conjuntos, una relación bien fundada sobre una clase X es una relación binaria R sobre X tal que todo subconjunto no vacío de X tiene un elemento R mínimo; esto es: Para todo subconjunto no vacío S de X, hay un elemento m en S tal… …   Wikipedia Español

  • Relación de equivalencia — Una relación de equivalencia sobre K es una relación binaria Relación de equivalencia que cumple las siguientes propiedades: ● Es reflexiva: ∀a ∈ K, a Relación de equivalencia a. ● Es simétrica: a Relación de equivalencia b ⇒ b Relación de equiva …   Enciclopedia Universal

  • Relación de equivalencia — …   Wikipedia Español

  • Clausura simétrica — Sea R una relación binaria aplicada sobre un conjunto A, la clausura simétrica o cierre simétrico de R, denotada CS(R), es la relación simétrica más pequeña aplicada sobre A que contiene a R. En otras palabras, CS(R) es la relación binaria que… …   Wikipedia Español

  • Clausura de relación — En matemática, sea una relación R sobre un conjunto A, la clausura o cierre de R es la menor relación que contiene a R y cumple con una propiedad dada. Tales propiedades pueden ser la transitividad, reflexividad o simetría, en cuyo caso la… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”