- Suma de Riemann
-
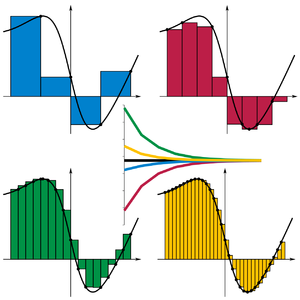Cuatro de los métodos de suma de Riemann para aproximar el área bajo las curvas. Los métodos derecha e izquierda hacen la aproximación usando, respectivamente, los puntos finales derechos e izquierdos de cada subintervalo. Los métodos máximo y mínimo hacen la aproximación usando, respectivamente, los valores más grandes y más pequeños del punto final de cada subintervalo. Los valores de las sumas convergen a medida que los subintervalos parten desde arriba a la izquierda hasta abajo a la derecha.
En matemáticas, la suma de Riemann es un método de integración numérica que nos sirve para calcular el valor de una integral definida es decir el área bajo una curva, este metodo es muy útil cuando no es posible utilizar el Teorema Fundamental del Cálculo. Estas sumas toman su nombre del matemático alemán Bernhard Riemann.
La suma de Riemann consiste básicamente en trazar un número finito de rectangulos dentro de un área irregular, calcular el área de cada uno de los rectangulos y sumarlos. El problema de este método de integración numérica es que al sumar las áreas se obtiene un margen de error muy grande.
Definición
Consideremos lo siguiente:
-
- una función
![f:[D]\rightarrow\mathbb{R}](3/293bb52f0a89d73cc4f24b6308e7471c.png)
- donde D es un subconjunto de los números reales
- una función
-
- I = [a, b] un intervalo cerrado contenido en D.
-
- Un conjunto finito de puntos {x0, x1, x2, ... xn} tales que a = x0 < x1 < x2 ... < xn = b
- crean una partición de I
- P = {[x0, x1), [x1, x2), ... [xn-1, xn]}
Si P es una partición con n elementos de I, entonces la suma de Riemann de f sobre I con la partición P se define como
- donde xi-1 ≤ yi ≤ xi. La elección de yi en este intervalo es arbitraria.
- Si yi = xi-1 para todo i, entonces denominamos S como la suma de Riemann por la izquierda.
- Si yi = xi, entonces denominamos S como la suma de Riemann por la derecha.
- Promediando las sumas izquierda y derecha de Riemann obtenemos la llamada suma trapezoidal.
Véase también
-
Wikimedia foundation. 2010.
