Geometría taxicab

Distancia Manhattan contra distancia Euclideana: Las líneas rojo, azul y amarillas tienen la misma longitud (12) en las geometrías Euclideana y taxicab. En la geometría Euclideana, la línea verde tiene longitud 6×√2 ≈ 8.48, y es el único camino más corto. En la geometría taxicab, la línea verde tiene longitud 12, por lo que no es más corta que los otros caminos.

La Geometría Taxicab, considerada por Hermann Minkowski en el siglo XIX, es una forma de geometría en la cual la métrica usual de la geometría euclideana es reemplazada por una nueva métrica en la cual la distancia entre dos puntos es la suma de las diferencias (absolutas) de sus coordenadas. La métrica taxicab también se conoce como distancia rectilínea, distancia L₁ o norma ₁ (ver Espacio L^p), distancia de ciudad, distancia Manhattan, o longitud Manhattan, con las correspondientes variaciones en el nombre de la geometría.^[1] El último nombre alude al diseño de grilla de la mayoría de las calles de la isla de Manhattan, lo que causa que el camino más corto que un auto puede tomar entre dos puntos de la ciudad tengan la misma distancia que dos puntos en geometría Taxicab.

Descripción formal

La distancia Taxicab, d₁, entre dos vectores en un espacio vectorial real n-dimensional con un sistema de Coordenadas cartesianas fijo es la suma de las longitudes de las proyecciones del segmento de línea entre los puntos sobre el sistema de ejes coordenados. Mas formalmente,

donde y son vectores.

Por ejemplo, en el plano, la distancia Taxicab entre (p₁,p₂) y (q₁,q₂) es | p₁ − q₁ | + | p₂ − q₂ | .

La distancia Taxicab depende de la rotación del sistema de coordenadas, pero no depende de su reflexión sobre un eje coordenado o su traslación. La geometría Taxicab satisface todos los axiomas de Hilbert (una formalización de la geometría Euclideana excepto por el axioma SAS), ya que uno puede generar dos triangulos con dos lados cada uno, y el ángulo entre ellos igual, y que no sean congruentes.

Círculos en geometry Taxicab discreta y continua.

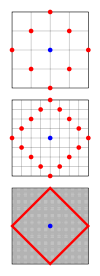
Un círculo es un conjunto de puntos con una distancia fija, llamada radio, desde un punto llamado centro. En la geometría Taxicab, la distancia es determinada por una métrica diferente que en la geometría Euclideana, y la forma de los círculos también cambia. Los círculos Taxicab son cuadrados con los lados orientados en un ángulo de 45° con los ejes coordenados. La imagen de la derecha muestra por qué esto es así, mostrando en rojo el conjunto de todos los puntos con una distancia fija desde un centro, mostrado en azul. Mientras el tamaño de los bloques de ciudad disminuye, los puntos se vuelven más numerosos y se convierten en un cuadrado rotado en una geometría Taxicab continua. Mientras que cada lado tendría una longitudo √2r usando una métrica Euclideana, donde r es el radio del círculo, su longitud en geometría Taxicab es 2r. Por lo tanto, la longitud de la circunferencia es 8r. La fórmula para el círculo unitario en geometría Taxicab es en coordenadas Cartesianas y r = 1 / (|sinθ| + |cosθ|) en coordenadas polares.

Un círculo de radio r por la distancia de Chebyshev (espacio métrico inyectivo.

Un círculo de radio 1 (usando esta distancia) es el vecindario von Neumann de su centro.

Medida de distancias en ajedrez

En el ajedrez, la distancia entre cuadrados en el tablero de ajedrez para las torres se mide en distancia Manhattan; reyes y reinas usan la distancia Chebyshev, y los alfiles usan la distancia Manhattan (entre cuadrados del mismo color) en el tablero rotado en 45 grados, es decir, con sus diagonales como ejes coordenados. Para ir de un cuadrado a otro, solo los reyers requieren tantos movimientos como el valor de la distancia; torres, reinas y alfiles requieren uno o dos movimientos (en un tablero vacío, y asumiendo que el movimiento es posible en el caso del alfil).

Véase también

• Espacio vectorial normado
• Espacio métrico
• Casco ortogonal convexo
• Distancia de Hamming
• Puzzle 15

Notes

References

• Eugene F. Krause (1987). Taxicab Geometry. Dover. ISBN 0-486-25202-7. 

Enlaces externos

• City Block Distance, por Kardi Teknomo
• city-block metric en PlanetMath
• Barile, Margherita. «Taxicab Metric» (en inglés). MathWorld. Wolfram Research.
• Manhattan distance. Paul E. Black, Dictionary of Algorithms and Data Structures, NIST
• Taxi! - columna en AMS sobre geometría Taxicab