Congruencia (geometría)

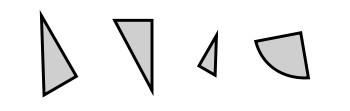Un ejemplo de movimiento o congruencia. Las dos figuras de la izquierda son congruentes, mientras que la tercera es semejante a ellas. La última no es ninguna de las dos cosas. Nótese que los movimientos cambian propiedades de las figuras como la posición y orientación de estas, pero dejan inalteradas otras como las distancias y los ángulos.

En ciertas áreas de la geometría, dos conjuntos de puntos son congruentes (o también, están relacionados por un movimiento) si existe una isometría que los relaciona: una transformación que es combinación de translaciones, rotaciones y reflexiones. Por así decirlo, dos figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u orientación sean distintas.

Ángulos congruentes

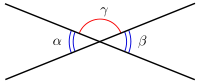
	Los ángulos α y β son congruentes y opuestos por el vértice.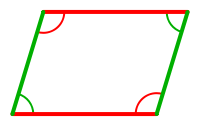
	Los ángulos opuestos de un paralelogramo son congruentes. En esta imagen podemos ver que están marcados por el mismo color.

Se denomina ángulos congruentes a aquellos ángulos que tienen la misma medida.

Los ángulos opuestos por el vértice son un ejemplo de ángulos congruentes. Las diagonales de un paralelogramo configuran ángulos opuestos por el vértice congruentes.

Congruencia de triángulos

La congruencia de triángulos estudia los casos en que dos o más triángulos presentan ángulos y lados de igual medida o congruentes.

Condiciones de congruencia

Para que se dé la congruencia de dos o más triángulos, se requiere que sus lados respectivos sean congruentes, es decir que tengan la misma medida. Esta condición implica que los ángulos respectivos también tienen la misma medida o son congruentes.

Las figuras congruentes son aquellas que tienen la misma forma y el mismo tamaño. Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.

Para corroborar que dos triángulos son congruentes se debe asegurar la congruencia de todos los lados de uno con todos los lados correspondientes del otro y la congruencia de todos los ángulos de uno con todos los ángulos correspondientes del otro.

Criterios de congruencia de triángulos

Dos triángulos son congruentes cuando sus tres lados y ángulos también lo son. Sin embargo, puede demostrarse la congruencia de dos triángulos si se sabe que algunas de sus partes correspondientes son homólogas.

Las condiciones mínimas que deben cumplir dos triángulos para que sean congruentes se denominan criterios de congruencia, los cuales son:

• Criterio LLL: Si en dos triángulos los tres lados de uno son respectivamente congruentes con los del otro, entonces los triángulos son congruentes.
• Criterio LAL: Si los lados que forman un ángulo, y éste, son congruentes con dos lados y el ángulo comprendido por estos de otro triángulo, entonces los triángulos son congruentes.
• Criterio ALA: Si dos ángulos y el lado entre ellos son respectivamente congruentes con los mismos de otro triángulo, entonces los triángulos son congruentes.

Véase también

• Geometría euclídea
• Isometría
• Triángulo
• Triángulos semejantes
• Teorema de Pitágoras

Otras relaciones aritméticas entre ángulos

• Ángulos complementarios
• Ángulos suplementarios

Relaciones posicionales entre ángulos

• Ángulos opuestos por el vértice
• Ángulos adyacentes

Referencias

• Este artículo fue creado a partir de la traducción del artículo Congruence (geometry) de la Wikipedia en inglés, concretamente de esta versión, bajo licencia Creative Commons Atribución Compartir Igual 3.0 y GFDL.

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre Congruencia (geometría). Commons
• http://www.uv.es/ivorra/Libros/Geometria.pdf
• The SSS en Cut-the-Knot
• The SSA en Cut-the-Knot