Uno de los grados posibles de separación es el de los espacios T₂ o Hausdorff, en que puntos diferentes siempre están separados por abiertos disjuntos.

La Topología es una rama de las matemáticas donde lo que importa no son los tamaños de las figuras ni las distancias entre sus puntos sino mas bien la forma de las figuras, así como las propiedades que se mantienen cuando estas figuras son deformadas (por ejemplo la cantidad de puntos en esta figura o la propiedad de ser "de una sola pieza"). Existen distintas maneras de clasificar esas propiedades; las más destacadas son: propiedades de compacidad, propiedades de conexión y propiedades de separación. Veamos en qué consisten estas propiedades de separación y como podemos distinguir espacios topológicos por medio de los llamados "axiomas de separación".

Los axiomas de separación constituyen unos requisitos adicionales que se pueden exigir a un espacio topológico. Estos requisitos fijan el grado en que distintos puntos o conjuntos cerrados pueden ser separados por medio de los abiertos de la topología.^[1]

Existen varios niveles crecientes de separación que se pueden pedir a un espacio topológico. Suelen denominarse con la letra T (de Trennung, separación en alemán) y un subíndice conveniente. Así aparece una jerarquía de espacios, entre los que cabe destacar a los espacios T₂ o espacios de Hausdorff, los T₃ o espacios regulares y los T₄ o espacios normales.

Por desgracia, salvo para T₀, T₁ y T₂, los nombres de los axiomas de separación no están completamente estandarizados.^[2]

Introducción

La definición de topología, en su generalidad, admite estructuras topológicas poco útiles: pensemos en un conjunto X con más de un elemento, dotado con la topología trivial (i.e. sus únicos abiertos son Ø y todo X). Esta topología no contiene abiertos que nos permitan distinguir topológicamente dos puntos diferentes: ambos puntos comparten el único entorno posible. Mirando los entornos abiertos de cada punto nos resulta imposible distinguirlos. Decimos que, a efectos topológicos, X no es diferente de un conjunto de un solo punto dotado de la topología trivial.^[3]

Necesitamos algún tipo de requisito sobre la topología que garantice un número suficiente de abiertos, de modo que éstos nos permitan distinguir topológicamente puntos distintos. Los diferentes grados en que se concreta esta exigencia se plasma en los diferentes axiomas de separación.

Algunos axiomas de separación

Espacios T₀ o Kolgomorov

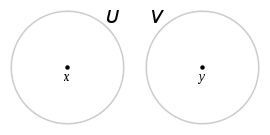
Un espacio topológico X se llama T₀ si y solo si para cualquier par de puntos 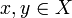existe un abierto que contiene uno de los puntos y no contiene el otro punto.

Una equivalencia a esta propiedad es la siguiente: si x,y son elementos del espacio X tales que la clausura de {x} y la clausura de {y} sean iguales entonces x = y

Espacios T₁ o Fréchet

Un espacio topológico X se dice espacios métricos son T₂), tienen propiedades fuertes como el que la convergencia de una sucesión o de un filtro, en caso de existir, sea única.

Espacios T₃ o regulares

Un espacio topológico X es regular si es T₀ y para cada punto 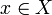y cualquier cerrado 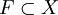tal que x no pertenece a F existe un entorno de x U_x y un entorno de F U_F tal que su intersección es vacía. Es decir, podemos separar puntos de cerrados.

Espacios 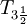, completamente regulares o Tychonoff

Un espacio topológico X es completamente regular si es T₀ y para cada punto 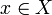y cualquier cerrado 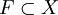tal que x no pertenece a F existe una funcion continua tal que f(x) = 0 y f(F) = 1.

Espacios T₄ o normales

Un espacio topológico X es normal si es T₁ y para cada par de cerrados 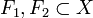con interseccion vacia existen unos entornos que los contengan 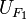y 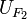tal que su intersección sea vacía. Es decir, podemos separar todos los cerrados del espacio. En particular los espacios métricos son normales.

Separación en espacios métricos

Es fácil verificar que 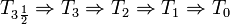. Es cierto que 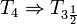, aunque esto no es tan evidente, es una consecuencia del Lema de Urysohn. Un espacio métrico (X,d) con su distancia asociada es normal, Tychonoff, regular, Hausdorff, Fréchet y finalmente Kolgomorov. Es importante destacar, para evitar errores, que el recíproco no es cierto.

Veamos que es cierto que todo espacio métrico es normal o T₄ y por consiguiente es Tychonoff, regular, Hausdorff, Fréchet y Kolgomorov.

Todo espacio métrico, con su distancia (X,d) es normal.

Demostración: Sean F₁ y F₂ dos cerrados de un espacio métrico X. Para cada 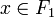sea r_x = d(x,F₂). Análogamente, para cada 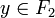sea s_y = d(y,F₁). Sea 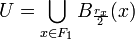, y sea 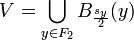. Es claro que tanto U, como V son abiertos, y que 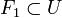y 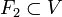. Se afirma que .

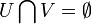Supongamos que es falso, entonces sea 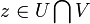. Quiere decir que existen x, y y tal que 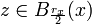y 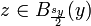. Pero eso implica que: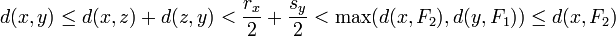

Lo cual es una contradicción.

Por tanto todos los espacios métricos son normales, y por tanto Tychonoff, regulares, Hausdorff, Fréchet y Kolgomorov.

Referencias