Variedad pseudoriemanniana

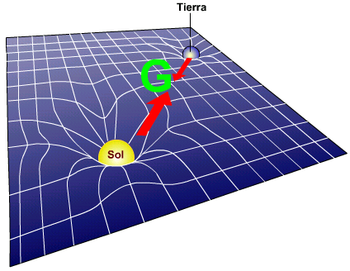Matemáticamente el espacio-tiempo curvo que usa la teoría de la relatividad es un variedad pseudoriemanniana con curvatura dada por la densidad de energía-impulso.

En geometría diferencial, una variedad pseudoriemanniana es una variedad diferenciable equipada con un tensor métrico (0,2)-diferenciable, simétrico, que es no degenerado en cada punto de la variedad. Este tensor se llama un tensor métrico pseudoriemanniano y a diferencia de un tensor métrico riemanniano no tiene por qué ser definido positivo. De hecho la variedades pseudoriemannianas generalizan el concepto de variedad riemannana

Un tipo especial de variedad pseudoriemanniana son las bandas lorentzianas o variedades de Lorentz (en honor a Hendrik Antoon Lorentz). Estas variedades tienen la propiedad de tener signatura (1,n-1) cuando la variedad tiene dimensión n. Las variedades lorentzianas tienen su interés en la teoría de la relatividad general, ya que uno de los supuestos básicos es que el espacio-tiempo puede modelizarse como una variedad pseudoriemanniana de cuatro dimensiones de signatura (1,3), es decir, la variedad pueda interpretarse como formada por 3 dimensiones espaciales y una temporal.

Variedades riemannianas y pseudoriemannianas

La diferencia clave entre una métrica Riemanniana y una métrica pseudoriemanniana es que una métrica pseudoriemanniana no necesita ser positiva-definida, simplemente no degenerada. Puesto que cada forma positivo-definida es también no degenerada una métrica Riemanniana es un caso especial de pseudoriemanniano. Así las variedades pseudoriemannianas se pueden considerar generalizaciones de las variedades de Riemann.

Cada forma no degenerada, simétrica bilineal tiene una signatura fija (p, q). Aquí p y q denotan el número de los valores propios positivos y negativos de la forma. La signatura de una variedad pseudoriemanniana es justa la signatura del métrico (uno debe insistir que la signatura está igual en cada componente conexo). Observe que p + q = n es la dimensión de la variedad. Los variedades de Riemann son simplemente ésos con la signatura (n, 0).

El espacio modelo para una variedad pseudoriemanniana de signatura (p, q) es R^{p, q} con la métrica

(1) ,

Algunos teoremas básicos de la geometría de Riemann se pueden generalizar al caso pseudoriemanniano. En particular, el teorema fundamental de la geometría de Riemann es verdad en las variedades pseudoriemannianas también. Esto permite que se hable de la conexión de Levi-Civita en una variedad pseudoriemanniana junto con el tensor asociado de curvatura. Por otra parte, hay muchos teoremas en la geometría de Riemann que no se sostienen en el caso generalizado. Por ejemplo, no es verdad que cada variedad diferenciable admite un métrica pseudoriemanniana de una signatura dada; hay ciertas obstrucciones topológicas.

Variedades de Lorentz

Las métricas pseudoriemannianas de signatura (p, 1) (o a veces (1, q), considerando la convención de signo) se llaman métricas de Lorentz. Un variedad equipada de una métrica de Lorentz naturalmente se llama una variedad de Lorentz. Después de las variedades de Riemann, las variedades de Lorentz, forman la subclase más importante de las variedades de Riemann. Son importantes debido a sus usos físicos para la teoría de la relatividad general. Una asunción principal de la relatividad general es que el espacio-tiempo se puede modelar como variedad de Lorentz de la signatura (3, 1).

Así pues, el espacio euclídeo Rⁿ se puede pensar como la variedad modelo de Riemann, el espacio de Minkowski R^p,1 con la métrica chata de Minkowski es la variedad modelo de Lorentz.

Una diferencia importante entre las variedades de Riemann y las variedades de Lorentz, es que en las primeras toda curva geodésica es un mínimo local de longitud, mientras que en una variedad lorentziana es un extremo local o una curva de "longitud cero" (un mínimo en el caso de geodésicas espaciales, un máximo en el caso de geodésicas temporales y una curva de "longitud" cero a lo largo de una geodésica lumínica).

Geodésicas

Una propiedad importante de las variedades pseudoriemannianas es que en ellas las curvas geodésicas o curvas de mínima curvatura no tienen por qué ser localmente curvas de mínima longitud, sino simplemente extremales de las ecuaciones de Euler-Lagrange, es decir, curvas que pueden ser localmente de máxima o de mínima "longitud" (de hecho, el nombre longitud puede ser incorrecto ya que nos referimos a una magnitud que generaliza la longitud de una curva y puede ser positiva, negativa o cero).

Bibliografía

• O'Neill, B. Semi-Riemannian Geometry: With Applications to Relativity. Academic Press, 1983.

ISBN 0-12-526740-1