Campo tensorial

Campo tensorial

Campo tensorial

Un campo tensorial es una asignación de una aplicación multilineal a cada punto de un dominio del espacio. En física llamamos también campo tensorial a cualquier magnitud física que puede ser representada por una asignación del tipo anterior definida sobre una región del espacio físico.


Campos tensoriales en matemática

Dado una región abierta y conexa Ω en Rn se define formalmente un campo tensorial a una aplicación (sección) cuyos valores son tensores:

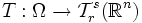
T: \Omega \rightarrow \mathcal{T}_r^s(\mathbb{R}^n)

Donde Trs es el conjunto de tensores r veces covariantes y s veces contravariantes. Decimos que T es un campo vectorial Ck si T es k veces continuamente diferenciable en Ω. Obsérvese que:

  1. Si (r, s) = (0,0) el campo tensorial es un campo escalar convencional.
  2. Si (r, s) = (1,0) o (0,1) el campo tensorial es un campo vectorial convencional.
  3. Si r+s = 2 el campo tensorial se puede visualizar como un espacio n-dimensional con una matriz de n×n unida a cada punto de Ω.

Campos tensoriales en física

Diversas magntiudes físicas vienen representadas por un campo tensorial, algunos ejemplos son:

Véase también

Obtenido de "Campo tensorial"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Campo (física) — Saltar a navegación, búsqueda En física, un campo es cualquier magnitud física que presenta cierta variación sobre una región del espacio. En ocasiones campo se refiere a una abstracción matemática para estudiar la variación de una cierta… …   Wikipedia Español

  • Campo eléctrico — producido por un conjunto de cargas puntuales. Se muestra en rosa la suma vectorial de los campos de las cargas individuales; . El campo eléctrico es un campo físico que es representado mediante un modelo que describe la interacció …   Wikipedia Español

  • Campo — Saltar a navegación, búsqueda Contenido 1 Medio rural 2 Deporte 3 Derecho 4 Física …   Wikipedia Español

  • Campo de color — Saltar a navegación, búsqueda El campo de color (o campo gluónico) es un campo físico asociado a la interacción fuerte entre partículas que llevan asociadas una carga de color. Desde el punto de vista matemático el campo de color se representa… …   Wikipedia Español

  • Campo gravitatorio — Saltar a navegación, búsqueda En física, el campo gravitatorio o campo gravitacional es un campo de fuerzas que representa la interacción gravitatoria. Si se dispone en cierta región del espacio una masa M, el espacio alrededor de M adquiere… …   Wikipedia Español

  • Campo espinorial — Saltar a navegación, búsqueda Un campo espinorial es un tipo de campo físico que generaliza los conceptos de campos vectoriales y tensoriales. Se caracteriza por dos peculiaridades: Las medidas obtenidas por dos observadores inerciales de un… …   Wikipedia Español

  • Campo vectorial — Ejemplo de campo vectorial no conservativo cuyo rotacional no se anula. En matemáticas, un campo vectorial representa la distribución espacial de una magnitud vectorial. Es una expresión de cálculo vectorial que asocia un vector a cada punto en… …   Wikipedia Español

  • Campo escalar — En matemáticas y física, un campo escalar representa la distribución espacial de una magnitud escalar, asociando un valor a cada punto del espacio. En matemáticas, el valor es un número; en física, una magnitud física. Los campos escalares se… …   Wikipedia Español

  • Campo electromagnético — Saltar a navegación, búsqueda Un Campo electromagnético es un campo físico, de tipo tensorial, que afecta a partículas con carga eléctrica. Fijado un sistema de referencia podemos descomponer convencionalmente el campo electromagnético en una… …   Wikipedia Español

  • Cálculo tensorial — Un tensor de segundo orden, en tres dimensiones. En matemáticas y en física, un tensor es cierta clase de entidad algebraica de varias componentes, que generaliza los conceptos de escalar, vector y matriz de una manera que sea independiente de… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”