Corchete de Lie (campos de vectores)

Corchete de Lie (campos de vectores)

Corchete de Lie (campos de vectores)

Para otros usos de este término, véase Corchete de Lie.

En topología diferencial, dados dos campos de vectores diferenciables X e Y sobre una variedad M, se define el corchete de Lie de los campos X e Y, notado [X,Y] como el único campo de vectores que cumple:

[X,Y](f)=X(Y(f))-Y(X(f))\,

Su expresión en un sistema de coordenadas asociado una carta local xμ será:

[X,Y]^i= \sum_{j=1}^n \left (X^j \frac {\partial Y^i}{\partial x^j} \right ) - \left ( Y^j \frac {\partial X^i}{\partial x^j} \right )

donde n es la dimensión de M.

El corchete de Lie de dos campos constituye un caso particular de una operación más general: la derivada de Lie de un tensor cualquiera 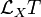\mathcal{L}_X T a lo largo de la dirección que marque un campo X. Cuando T es un campo de vectores Y, recuperamos el corchete de Lie

\mathcal{L}_X Y = [X,Y].

Propiedades

  • [.,.] es 'R-bilineal:
[\alpha X_1 + \beta X_2, Y] = \alpha [X_1, Y] + \beta [X_2, Y]\,,
[X, \alpha Y_1 + \beta Y_2] = \alpha [X, Y_1] + \beta [X, Y_2]\,,
  • Antisimetría:
[X,Y]=-[Y,X]\,
[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0.\,
  • Para funciones f y g tenemos
[fX, gY] = fg [X,Y] + fX(g) Y - gY(f) X\,.

Esta última igualdad destaca que aunque el corchete sea R-bilineal, no es bilineal sobre las funciones diferenciables. Como consecuencia, el corchete no tendrá carácter tensorial, es decir, el valor del vector [X,Y]p no solo dependerá del valor de los vectores Xp e Yp (no podremos definir el corchete de Lie de dos vectores), sino de los campos X e Y.

Como consecuencia inmediata de la antisimetría, [X,X] = 0 para cualquier campo X.

Coeficientes de estructura

Si {ek} una base local de campos de vectores, podremos desarrollar el corchete de dos de sus elementos como combinación lineal de los elementos de la base:

[e_k,e_\ell] = c_{k\ell}{}^m e_m\,\

A las funciones 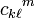c_{k\ell}{}^m se les denomina coeficientes de estructura de la base {ek}. Estos coeficientes no forman parte de un tensor.

En el caso especial en que la base esté asociada a un sistema de coordenadas {xa}, dado que los vectores básicos conmutan ( [\partial_{x^a},\partial_{x^b}]=0), los coeficientes de estructura serán nulos. Las bases locales para las que se anulan estos coeficientes reciben el nombre de bases holónomas.

En un grupo de Lie G, considerado como variedad, podemos definir un conjunto particular de campos de vectores: los campos invariantes por la izquierda. A este conjunto se le denomina álgebra de Lie de G. Dada una base 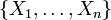\{X_1, \ldots , X_n\} de campos invariantes por la izquierda, se demuestra que los coeficientes de estructura son constantes, y reciben el nombre de constantes de estructura de G con respecto a la base {Xi}.

Véase también

Obtenido de "Corchete de Lie (campos de vectores)"

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Corchete de Lie — Saltar a navegación, búsqueda Corchete de Lie suele designar a una operación binaria notada por [ , ], que: Al superponerse a la estructura de espacio vectorial, junto con unas condiciones de compatibilidad entre operaciones, define una… …   Wikipedia Español

  • Corchete de Poisson — Saltar a navegación, búsqueda En matemáticas y mecánica clásica, el corchete de Poisson es un importante operador de la mecánica hamiltoniana, actuando como pieza fundamental en la definición de la evolución temporal de un sistema dinámico en la… …   Wikipedia Español

  • Grupo de Lie — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Derivada de Lie — Saltar a navegación, búsqueda En matemática, una derivada de Lie es una derivación en el álgebra de funciones diferenciables sobre una variedad M, cuya definición puede extenderse al álgebra tensorial de la variedad. Obtenemos entonces lo que en… …   Wikipedia Español

  • Tensor de curvatura — En geometría diferencial, el tensor de curvatura de Riemann , o simplemente tensor de curvatura o tensor de Riemann, supone una generalización del concepto de curvatura de Gauss, definido para superficies, a variedades de dimensiones arbitrarias …   Wikipedia Español

  • Álgebra sobre un cuerpo — En matemáticas, un álgebra sobre un cuerpo K, o una K álgebra, es un espacio vectorial A sobre K equipado con una noción compatible de multiplicación de elementos de A. Una generalización directa admite que K sea cualquier anillo conmutativo.… …   Wikipedia Español

  • Álgebra de Witt — En matemáticas el complejo llamado álgebra de Witt (en homenaje a quien la estudió: Ernst Witt) es un álgebra de Lie de campos vectoriales meromórficos definidos en la esfera de Riemann que es holomórfica excepto en dos puntos fijos. También la… …   Wikipedia Español

  • Grupo especial unitario — En matemáticas, el grupo especial unitario (o grupo unitario especial) de grado n es el grupo de matrices unitarias n por n con determinante igual a 1, con las entradas en el cuerpo C de los números complejos y con la operación de grupo dada por… …   Wikipedia Español

  • Símbolos de Christoffel — En matemáticas y física, los símbolos de Christoffel, así nombrados por Elwin Bruno Christoffel (1829 1900), son expresiones en coordenadas espaciales para la conexión de Levi Civita derivada del tensor métrico. Se utilizan los símbolos de… …   Wikipedia Español

  • Variedad (matemática) — En una esfera, la suma de los ángulos de un triángulo no es igual a 180°, pues una esfera no es un espacio euclídeo. Sin embargo, localmente, las leyes de la geometría euclídea son buenas aproximaciones. Este ejemplo ilustra cómo la esfera puede… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”