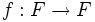- Cuerpo finito
-
Cuerpo finito
En álgebra abstracta, un cuerpo finito, campo finito o campo de Galois (llamado así por Évariste Galois) es un cuerpo que contiene un número finito de elementos. Los cuerpos finitos son importantes en teoría de números, geometría algebraica, teoría de Galois, y criptografía. Los cuerpos finitos son totalmente conocidos, y serán descritos más abajo.
Contenido
Clasificación
Dado que todo cuerpo de característica 0 contiene a los racionales y es por lo tanto infinito, todos los campos finitos tienen característica prima, y por lo tanto, su tamaño (o cardinalidad) es de la forma pn, para p primo y n > 0 entero (pues el campo es un espacio vectorial sobre el subcuerpo de cardinalidad p generado por el elemento 1). No es en general cierto, sin embargo, que todo cuerpo de característica prima sea finito.
Para un primo p, los enteros módulo p forman un cuerpo de p elementos, denotado por Z/pZ (pues su grupo aditivo es isomorfo al grupo cíclico de p elementos), Fp, o GF(p); en algunos casos se usa Zp, aunque esta notación es evitada por teoristas de los números, pues puede crear confusión con el anillo de los números p-ádicos. Todo cuerpo con p elementos es isomorfo a éste.
Si q = pn es una potencia de un primo, existe (salvo isomorfismo) exactamente un campo con q elementos, denotado por Fq o GF(q). Se puede construir como sigue: encuéntrese un polinomio irreducible f(X) de grado n con coeficientes en Fp, y defínase Fq = Fp[X] / <f(T)>, donde Fp[X] denota el anillo de todos los polinomios con coeficientes en Fp, <f(X)> denota el ideal generado por f(X), y la barra diagonal indica el anillo cociente (definido de forma similar al grupo cociente). El polinomio f(X) se puede hallar factorizando Xq-X sobre Fp. El campo Fq contiene a (una copia de) Fp como subcampo.
No hay otros campos finitos.
Ejemplos
El polinomio f(X) = X2 + X + 1 es irreducible en F2, y F4 = F2[X] / <X2 + X + 1> puede representarse como el conjunto {0, 1, x, x+1} donde la multiplicación queda definida por la ecuación x2 + x + 1 = 0. Por ejemplo, para hallar x3, se observa que x(x2 + x + 1) = 0, con lo cual x3 + x2 + x = 0, y x3 = -x2 - x = (x + 1)( - x) = 1; de forma equivalente, habiendo observado que x3 + x2 + x = 0, se obtiene que x3 + (x2 + x + 1) = 1 con lo que x3 = 1, como antes.
Para encontrar un inverso multiplicativo de x en este campo, se debe encontrar un polinomio g(X) tal que X * g(X) = 1 módulo X2 + X + 1; el polinomio g(X) = X + 1 cumple esta propiedad, de modo que 1/x = x + 1.
Obsérvese que el campo F4 no tiene relación con el anillo Z4 de enteros módulo 4.
Para construir el campo F27, se comienza con el polinomio irreducible (en F3) X3 + X2 + X - 1. Se tiene entonces F27 = {ax2 + bx + c | a, b, c ∈ F3}, donde la multiplicación se define por
x3 + x2 + x - 1 = 0 (de la misma manera que en el ejemplo pasado).
Propiedades
Si F es un campo finito con q = pn elementos (con p primo), entonces
- xq = x
para todo x ∈ F. Más aún, la función
definida por
- f(x): = xp
es biyectiva y un homomorfismo, con lo cual es un automorfismo de F. Se la llama automorfismo de Frobenius, en honor a Ferdinand Georg Frobenius.
El automorfismo de Frobenius tiene orden n, y por lo tanto el grupo cíclico generado por éste es el grupo completo de automorfismos del campo.
El campo Fpm contiene una copia de Fpn si y sólo si n divide a m. La razón para la dirección "si" es que hay polinomios irreducibles de cualquier grado en Fpm.
Si se construyen los campos finitos de forma tal que Fpn esté efectivamente contenido en Fpm siempre que n divida a m, se puede tomar la unión de todos esos campos; ésta es también un campo de característica p, aunque infinito. Es la clausura algebraica de cada uno de los campos Fpn. Aun si no se construyen de esta manera los campos, se puede hablar de su clausura algebraica, aunque su construcción es ahora más delicada.
Aplicaciones
El grupo multiplicativo de todo cuerpo finito es cíclico. Esto significa que si F es un campo finito de q elementos, siempre hay un elemento x ∈ F tal que F = { 0, 1, x, x2,..., xq-2 }.
El elemento x no es único. Si se toma uno en particular, entonces para todo a ≠ 0 en F hay un único n ∈ {0,..., q - 2} tal que a = xn. El valor de n para un dado a se llama logaritmo discreto de a en base x. En la práctica, aunque calcular xn es relativamente trivial dado n, encontrar n para un a dado es un proceso computacionalmente difícil, por lo que tiene muchas aplicaciones en criptografía.
Los primeros cuerpos finitos
F2:
+ | 0 1 · | 0 1 --+---- --+---- 0 | 0 1 0 | 0 0 1 | 1 0 1 | 0 1
F3:
+ | 0 1 2 · | 0 1 2 --+------ --+------ 0 | 0 1 2 0 | 0 0 0 1 | 1 2 0 1 | 0 1 2 2 | 2 0 1 2 | 0 2 1
F4:
+ | 0 1 A B · | 0 1 A B --+-------- --+-------- 0 | 0 1 A B 0 | 0 0 0 0 1 | 1 0 B A 1 | 0 1 A B A | A B 0 1 A | 0 A B 1 B | B A 1 0 B | 0 B 1 A
Categoría: Álgebra abstracta
Wikimedia foundation. 2010.