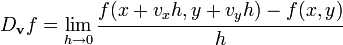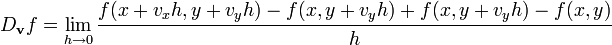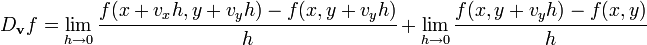Derivada direccional

Derivada direccional

Derivada direccional

En el Análisis matemático, la derivada direccional de una función multivariable sobre un vector dado, representa la tasa de cambio (pendiente) de la función en la dirección de dicho vector. Este concepto generaliza a las derivadas parciales, ya que estas son derivadas direccionales en los vectores paralelos a los ejes.

Contenido

Funciones escalares reales

La derivada direccional de una función 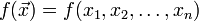f(\vec{x}) = f(x_1, x_2, \ldots, x_n) sobre un vector unitario 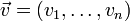\vec{v} = (v_1, \ldots, v_n) es la función definida por este límite: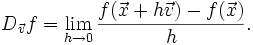

D_{\vec{v}}{f} = \lim_{h \rightarrow 0}{\frac{f(\vec{x} + h\vec{v}) - f(\vec{x})}{h}}.

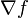
Si la función es diferenciable, puede ser escrita en término de su gradiente \nabla f

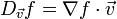
D_{\vec{v}}{f} = \nabla f \cdot \vec{v}

donde \cdot denota el producto escalar o producto punto entre vectores.

Demostración

El caso más sencillo de la derivada direccional se da en el espacio tridimensional. Supongase que se tiene una función diferenciable 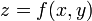z = f(x,y)\;. La derivada direcciónal según la dirección de un vector 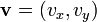\mathbf{v} = (v_x,v_y) sería:

D_\mathbf{v}f = \lim_{h\to 0} \cfrac{f(x+v_xh,y+v_yh)-f(x,y)}{h}
D_\mathbf{v}f = \lim_{h\to 0} \cfrac{f(x+v_xh,y+v_yh)-f(x,y+v_yh)+f(x,y+v_yh)-f(x,y)}{h}
D_\mathbf{v}f = \lim_{h\to 0} \cfrac{f(x+v_xh,y+v_yh)-f(x,y+v_yh)}{h} + \lim_{h\to 0} \cfrac{f(x,y+v_yh)-f(x,y)}{h}


El primero de estos límites puede calcularse mediante el cambio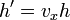 h' = v_xh\; lo cual lleva, por ser diferenciable la función[1] f, a: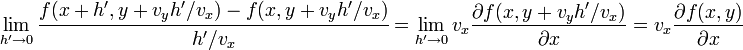

\lim_{h'\to 0} \cfrac{f(x+h',y+v_yh'/v_x)-f(x,y+v_yh'/v_x)}{h'/v_x} = \lim_{h'\to 0} v_x\frac{\part f(x,y+v_yh'/v_x)}{\part x} = v_x\frac{\part f(x,y)}{\part x}

Procediendo análogamente para el otro límite se tiene que:

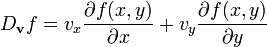
D_\mathbf{v}f = v_x\frac{\part f(x,y)}{\part x} + v_y\frac{\part f(x,y)}{\part y}

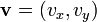Resultado que trivialmente coincide con el producto escalar del gradiente por el vector \mathbf{v} = (v_x,v_y):

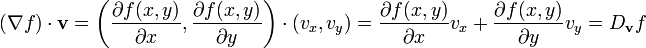
(\nabla f)\cdot\mathbf{v} = \left(\frac{\part f(x,y)}{\part x}, \frac{\part f(x,y)}{\part y} \right) \cdot (v_x,v_y) = \frac{\part f(x,y)}{\part x}v_x + \frac{\part f(x,y)}{\part y}v_y = D_\mathbf{v}f

Campos vectoriales

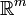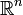El concepto de derivada direccional se puede generalizar a funciones de \mathbb{R}^m en \mathbb{R}^n, del tipo: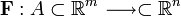

\mathbf{F}:A\subset\mathbb{R}^m \longrightarrow \subset\mathbb{R}^n

En este caso la derivada direccional de modo idéntico a como se hacía con funciones de una variable:

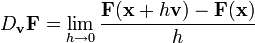
D_\mathbf{v}\mathbf{F} = \lim_{h\to 0} \frac{\mathbf{F}(\mathbf{x}+h\mathbf{v})-\mathbf{F}(\mathbf{x})}{h}

Una diferencia con el caso de funciones de reales de una variable es que la existencia de derivadas direccionales según todas las direcciones no implica necesariamente que una función sea diferenciable. Si la función es diferenciable resulta que la aplicación:

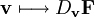
\mathbf{v} \longmapsto D_\mathbf{v}\mathbf{F}

Es lineal y se cumple además es expresable en términos del jacobiano:

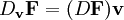
D_\mathbf{v}\mathbf{F} = (D\mathbf{F})\mathbf{v}

Funcionales

Artículo principal: derivada funcional

La derivada funcional, definida como derivada de Gâteaux, es de hecho una derivada direccional definida en general sobre un espacio vectorial de funciones.

Referencias

  1. ↑ Si la función no es diferenciable entonces las derivadas parciales no son continuas y esta demostración no es válida, Bombal, R. Marín, Vera, p. 4
  • Bombal, R. Marín & Vera: Problemas de Análisis matemático: Cálculo Diferencial, 1988, ed. AC, ISBN 84-7288-101-6.

Véase también

Obtenido de "Derivada direccional"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Derivada funcional — Saltar a navegación, búsqueda En las matemática y la física teórica, la derivada funcional es una generalización de la derivada usual que se presenta en el cálculo de variaciones. En una derivada funcional, en vez de diferenciar una función con… …   Wikipedia Español

  • Derivada — La derivada de la función en el punto marcado equivale a la pendiente de la recta tangente (la gráfica de la función está dibujada en negro; la tangente a la curva está dibujada en rojo). En matemáticas, la derivada de una función es una medida… …   Wikipedia Español

  • Variedad diferenciable — En Geometría y Topología, una variedad diferenciable es un tipo especial de variedad topológica, a la que podemos extender las nociones de cálculo diferencial que normalmente usamos en . En una variedad diferenciable M podremos definir lo que es… …   Wikipedia Español

  • Gradiente — En cálculo vectorial, el gradiente de un campo escalar f es un campo vectorial. El vector gradiente de f evaluado en un punto genérico x del dominio de f, (x), indica la dirección en la cual el campo f varía más rápidamente y su módulo representa …   Wikipedia Español

  • Cálculo tensorial — Un tensor de segundo orden, en tres dimensiones. En matemáticas y en física, un tensor es cierta clase de entidad algebraica de varias componentes, que generaliza los conceptos de escalar, vector y matriz de una manera que sea independiente de… …   Wikipedia Español

  • Gradiente — (Del lat. gradiens, ntis, el que anda.) ► sustantivo masculino 1 FÍSICA Relación de diferencia de temperatura y presión barométrica entre dos puntos. ► sustantivo femenino 2 Chile, Ecuador, Nicaragua, Perú Pendiente, declive o repecho de un… …   Enciclopedia Universal

  • Glosario de relatividad — Anexo:Glosario de relatividad Saltar a navegación, búsqueda Este artículo contiene un glosario términos comúnmente usados en teoría de la relatividad. Se definen algunos de los términos brevemente y se enlaza a un artículo más amplio si éste… …   Wikipedia Español

  • Anexo:Glosario de relatividad — Este artículo contiene un glosario términos comúnmente usados en teoría de la relatividad. Se definen algunos de los términos brevemente y se enlaza a un artículo más amplio si éste existe. Índice: A B C D E F G H I J K L M N Ñ O P Q R S T U V W… …   Wikipedia Español

  • Equilibrio de Gibbs Donnan — Saltar a navegación, búsqueda Esquema para el equilibrio de Gibbs Donnan El equilibrio de Gibbs Donnan es el equilibrio que se produce entre los iones que pueden atravesar la membrana y los que no son capaces de hacerlo. Se juega con los iones y… …   Wikipedia Español

  • Gradiente (desambiguación) — El término gradiente puede hacer referencia a: En matemáticas, el gradiente de un campo escalar en un punto es un vector, definido como el único que permite hallar la derivada direccional en cualquier dirección. Gradiente térmico: número de… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”