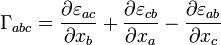- Ecuación de compatibilidad
-
Ecuación de compatibilidad
Una ecuación de compatibilidad es una ecuación adicional a un problema mecánico de equilibrio necesaria para asegurar que la solución buscada es compatible con las condiciones de contorno o para poder asegurar la integrabilidad del campo de deformaciones.
Contenido
Ecuaciones de compatibilidad en deformaciones
En el planteamiento del problema elástico, las ecuaciones de compatibilidad son ecuaciones que si se cumplen garantizan la existencia de un campo de desplazamientos compatible con las deformaciones calculadas. En otras palabras, las ecuaciones de compatibilidad son las condiciones necesarias de integrabilidad para el campo de desplazamientos en términos de las componentes del tensor tensión.
Elasticidad lineal
En elasticidad lineal una deformación será físicamente posible si es compatible con un determinado campo de desplazamientos
 es decir si se cumplen las siguientes relaciones para las componentes del tensor deformación:
es decir si se cumplen las siguientes relaciones para las componentes del tensor deformación: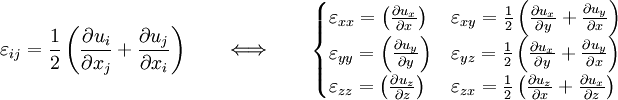
Normalmente las componentes del campo de desplazamiento son desconocidas por lo que necesitamos una relación expresable sólo en términos de las componentes del tensor deformación. La expresión buscada es precisamente:[1]
(1)
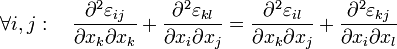
Estas últimas relaciones son precisamente las que se conocen como ecuaciones de compatibilidad de la elasticidad lineal.
Elasticidad no-lineal
En teoría de la elasticidad no lineal la relación entre el vector de desplazamientos y las componentes del tensor tensión son no lineales y substancialmente más complicadas:
![\varepsilon_{ij} = \frac{1}{2}\left[\frac{\part u_i}{\part x_j}+ \frac{\part u_j}{\part x_i} +
\sum_k \left(\frac{\part u_k}{\part x_i}+ \frac{\part u_k}{\part x_j}\right) \right]](/pictures/eswiki/56/8c51bae7ecf730844c7e9d5308f44b5f.png)
Por lo que las ecuaciones de compatibilidad en elasticidad no lineal también son no-lineales:
(2)
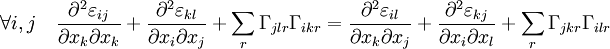
Donde los símbolos de Christoffel vienen dados por:
Ecuaciones de compatibilidad en desplazamientos
Con frecuencia, en problemas mecánicos o de resistencia de materiales hiperestáticos el cálculo de alguna fuerza u otra magnitud resulta insuficiente a partir de las condiciones de equilibrio. En ese caso, las ecuaciones de equilibrio forman un sistema compatible indeterminado. Puesto que la situación física real sí presenta una solución unívoca, es decir, las piezas mecánicas toman valores de tensión concretos y las reacciones reales tienen valores totalmente determinados, concluimos que las ecuaciones de equilibrio deben ser complementadas con algún otro tipo de información adicional que haga que el problema sea determinado.
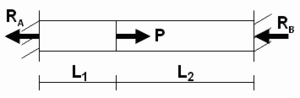
De hecho, muchos problemas se vuelven completamente determinados si tenemos en cuenta que los desplazamientos observados en la realidad tienen valores determinados. Así si introducimos ecuaciones que expresen ciertos desplazamientos en función del resto de variables, podemos llegar a construir un sistema de ecuaciones compatible determinado. Dicho sistema estaría formado por la ecuaciones de equilibrio, y varias ecuaciones adicionales llamadas ecuaciones de compatibilidad. Por ejemplo en la figura (Fig. 1) se muestra un problema unidimensional consistente en la aplicación de una fuerza en un punto intermedio empotrado en sus extremos. En este caso, el problema es estáticamente indeterminado o hiperestático el análisis de fuerzas lleva a una única ecuación para las dos reacciones incógnita existentes:
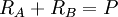
En este caso P es una fuerza conocida. Para poder determinar las reaciones observamos que la parte izquierda (entre RA y P) está traccionada y por tanto se estirará, mientras que la parte derecha (entre P y RB) está comprimida y por tanto se encogerá. Puesto que la pieza es un único sólido deformable el estiramiento de parte izquierda compensará exactamente el estiramiento de la parte derecha, de lo contrario la pieza se rompería. Por tanto estiramiento y acortamiento deben ser compatibles, ésa es precisamente la condición de compatibilidad adicional que resuelve el problema:
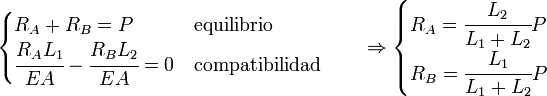
Las ecuaciones adicionales pueden obtenerse por diversos métodos, por ejemplo usando el teoremas de Castigliano o usando la ecuación de la curva elástica. Si el problema es suficientemente sencillo, como en el ejemplo anterior, puede encontrarse la ecuación de compatibilidad directamente.
Bibliografía
- ↑ Ortiz Berrocal, 1998, pág. 94-96.
- Timoshenko, Stephen; Godier J.N. (1951). McGraw-Hill (ed.). Theory of elasticity.
- Ortiz Berrocal, Luis (1998). McGraw-Hill (ed.). Elasticidad, pp. 94-96. ISBN 84-481-2046-9.
- Olivella, X.; Agelet de Saracibar, C. (2000). «3», Edicions UPC (ed.). Mecánica de Medios Continuos para Ingenieros, pp. 71-75. ISBN 978-84-8301-412-7.
Categorías: Mecánica de medios continuos | Resistencia de materiales
Wikimedia foundation. 2010.