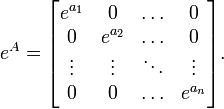Exponencial de matrices

Exponencial de matrices

Exponencial de matrices

La exponencial de matrices es una función definida sobre las matrices cuadradas, parecida a la función exponencial. Sea X una matriz nxn de números reales o complejos. La exponencial de X denotada por eX o exp(X) es la matriz nxn dada por la serie de potencias

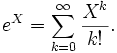
e^X = \sum_{k=0}^\infty \frac{X^k}{k!}.

Esta serie converge para toda matriz X. Obsérvese que si la matriz X es una matriz 1x1 la exponencial de X corresponde con la exponencial ordinaria.

Contenido

Propiedades

Sean X e Y dos matrices nxn, a y b dos números complejos cualesquiera. Denotemos con I a la matriz identidad y con 0 la matriz nula. Entonces

  1. Matriz identidad: e^0 = I\,.
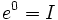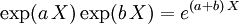  2. Linealidad: \exp(a\,X)\exp(b\,X) = e^{(a+b)\,X}.
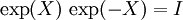  3. \exp(X)\,\exp(-X) = I. Esta es consecuencia de las dos anteriores.
  4. Matriz inversa: 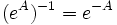(e^A)^{-1} = e^{-A}\; consecuencia de la anterior.
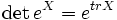  5. Relación traza-determinante: \det e^X = e^{tr X}\,.
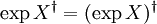  6. \exp{X^\dagger} = (\exp X)^\dagger, donde 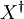X^\dagger denota la transpuesta de la matriz X.
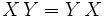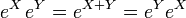  7. Preservación de la comuntación: Si X\,Y = Y\,X entonces e^X\,e^Y = e^{X+Y} = e^Ye^X.
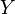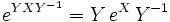  8. Si Y\, es invertible entonces e^{YXY^{-1}} = Y\,e^X\,Y^{-1}.
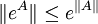
  9. Acotación de la norma: \|e^A\| \le e^{\|A\|}

Se sigue que si X es simétrica, entonces su exponencial también lo es. Si X es antisimétrica su exponencial es ortogonal.

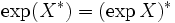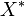  • \exp(X^*) = (\exp X)^*\, donde X^*\, denota la conjugada transpuesta de X.

Se sique que si X es hermítica entonces su exponencial también lo es. Si X es antihermítica entonces su exponencial es unitaria.

Cálculo de la exponencial de matrices

Matrices diagonales y diagonalizables

Si una matriz A es diagonal:

A=\begin{bmatrix} a_1 & 0 & \ldots & 0 \\ 0 & a_2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & a_n \end{bmatrix},

entonces su exponencial se obtiene tomando las exponenciales de cada uno de los elementos de la diagonal principal:

e^A=\begin{bmatrix} e^{a_1} & 0 & \ldots & 0 \\ 0 & e^{a_2} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & e^{a_n} \end{bmatrix}.

Una matriz 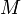M\; es diagonalizable entonces: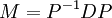

M = P^{-1} D P\;

Donde 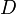D\; es una matriz diagonal y es un matriz no singular 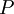P\; puede elegirse como una matriz unitaria. La exponenciación de matrices diagonalizables puede reducirse al caso de la exponencial de una matriz diagonal, sin más que usar la propiedad 5 mencionada arriba tenemos: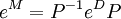

e^M = P^{-1} e^D P\;

Matrices que admiten forma de Jordan

La exponencial de una matriz que tiene de bloque de Jordan es muy sencilla:

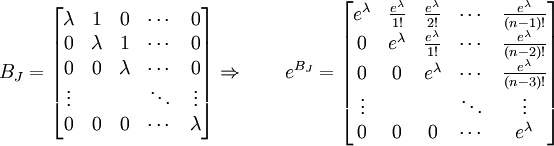
B_J = \begin{bmatrix} \lambda & 1 & 0 & \cdots & 0\\ 0 & \lambda & 1 & \cdots & 0\\ 0 & 0 & \lambda & \cdots & 0\\ \vdots & & & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & \lambda\end{bmatrix} \Rightarrow \qquad e^{B_J} = \begin{bmatrix} e^\lambda & \frac{e^\lambda}{1!} & \frac{e^\lambda}{2!} & \cdots & \frac{e^\lambda}{(n-1)!}\\ 0 & e^\lambda & \frac{e^\lambda}{1!} & \cdots & \frac{e^\lambda}{(n-2)!}\\ 0 & 0 & e^\lambda & \cdots & \frac{e^\lambda}{(n-3)!}\\ \vdots & & & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & e^\lambda \end{bmatrix}

Se dice que una matriz 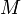M\; admite forma canónica de Jordan 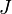J\; cuando existe otra matriz no singular tal que: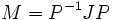

M = P^{-1} J P\;

Siendo 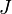J\; una matriz triangular formada por bloques de Jordan (es decir, cuya diagonal principal contiene los autovalores de 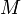M\; y sólo la diagonal superior a la principal tiene algunos "1"). En ese caso la exponencial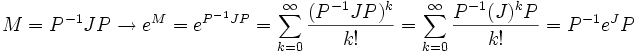

M=P^{-1}J P \to e^M = e^{P^{-1}J P} = \sum_{k=0}^\infty \frac{(P^{-1}J P)^k}{k!} = \sum_{k=0}^\infty \frac{P^{-1}(J)^k P}{k!} = P^{-1}e^{J}P

Aplicaciones

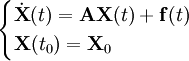
\begin{cases} \dot\mathbf{X}(t) = \mathbf{A}\mathbf{X}(t)+\mathbf{f}(t) \\ \mathbf{X}(t_0) = \mathbf{X}_0 \end{cases}

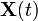Donde \mathbf{X}(t) representa el vector de funciones incógnita. La solución de este sistema viene dada por la exponenciación de la matriz de coeficientes:

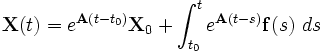
\mathbf{X}(t) = e^{\mathbf{A}(t-t_0)}\mathbf{X}_0 + \int_{t_0}^t e^{\mathbf{A}(t-s)}\mathbf{f}(s)\ ds

Véase también

Obtenido de "Exponencial de matrices"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Exponencial de una matriz — La exponencial de matrices es una función definida sobre las matrices cuadradas, parecida a la función exponencial. Sea una matriz nxn de números reales o complejos, la exponencial de denotada por o es la matriz dada por la serie de potencia …   Wikipedia Español

  • Exponenciación — Saltar a navegación, búsqueda La exponenciación es una operación definible en un álgebra sobre un cuerpo normada completa o álgebra de Banach (espacio vectorial normado completo que además es un anillo) que generaliza la función exponencial de… …   Wikipedia Español

  • Logaritmo de una matriz — En matemática, el logaritmo de una matriz es una función matricial que generaliza el logaritmo escalar a matrices. En cierto sentido es la función inversa de la exponenciación de matrices. Contenido 1 Definición 2 Propiedades 3 Cálculo del… …   Wikipedia Español

  • Grupo uniparamétrico — En matemáticas, un grupo uniparamétrico o subgrupo uniparamétrico es un subconjunto de un grupo de Lie de dimensión uno. De hecho un grupo uniparamétrico puede ser representado por una colección de operadores o elementos de un grupo , que vienen… …   Wikipedia Español

  • Grupo de Lie — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Vector propio y valor propio — Fig. 1. En esta transformación de la Mona Lisa, la imagen se ha deformado de tal forma que su eje vertical no ha cambiado. (nota: se han recortado las esquinas en la imagen de la derecha) …   Wikipedia Español

  • MATLAB — Desarrollador MathWorks www.mathworks.com/products/matlab …   Wikipedia Español

  • Raíz cuadrada — Expresión matemática de raíz cuadrada de X . La …   Wikipedia Español

  • Visual servoing — Contenido 1 1. METODOLOGÍAS DEL VISUAL SERVOING 2 1.1. Componentes básicos del VS 3 1.2. Visual servo basado en imagen (IBVS) 3.1 …   Wikipedia Español

  • Lagrangiano — En física, un lagrangiano es una función matemática a partir de la cual se pueden obtener la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico. De hecho, en física moderna el lagrangiano se… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”