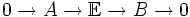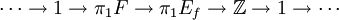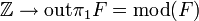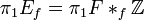Extensión de grupo

Extensión de grupo

Extensión de grupo

En el álgebra abstracta extender un grupo A con otro B es construir otro grupo 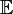\mathbb{E} que hace que la sucesión corta

0\to A\to\mathbb{E}\to B\to 0

sea exacta.

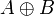Ejemplo de una tal extensión es la suma directa A\oplus B.

Es sabido que los homomorfismos (de grupo) 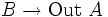B\to {\rm Out}\ A los clasifican. Aquí la construcción 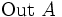{\rm Out}\ A es el conjunto de automorfismos exteriores, definido como el cociente

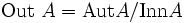{\rm Out}\ A={\rm Aut} A/{\rm Inn} A.

Ejemplo

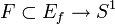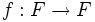Considere el fibrado F\subset E_f\to S^1 donde f:F\to F es un auto-homeomorfismo de la superficie F, entonces desde la sequencia homotópica larga del fibrado tenemos el tramo:

\cdots\to 1\to\pi_1F\to\pi_1E_f\to\mathbb{Z}\to1\to\cdots

Pero como sabemos que los homomorfismos de grupo:

\mathbb{Z}\to{\rm out}\pi_1F={\rm mod}(F)

clasifican a estas extensiones y donde el generador de 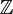\mathbb{Z} es asignado al auto-homeomorfismo f, entonces tenemos que el grupo fundamental del fibrado E está dado por

\pi_1E_f=\pi_1F*_f\mathbb{Z}

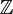es decir, estamos extendiendo el grupo fundamental de la superficie F por el subgrupo cíclico infinito \mathbb{Z}.

Es conocido que tales grupos tiene una presentación de la forma 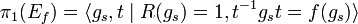\pi_1(E_f)=\langle g_s,t\mid R(g_s)=1, t^{-1}g_st=f(g_s)\rangle que corresponde a una HNN extensión del grupo fundamental de la superficie F.

Referencias

  • A.G. Kurosch. The theory of groups. Chelsea, 2 vols. 1955-1956.
  • M.Hall. The theory of groups. Macmillan. 1959.
Obtenido de "Extensi%C3%B3n de grupo"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Extensión de Galois — Saltar a navegación, búsqueda En álgebra abstracta, una extensión de cuerpo algebraica E/K se dice extensión de Galois (o extensión galoisiana) si es una extensión normal y separable. En este caso, se puede considerar el grupo de Galois de la… …   Wikipedia Español

  • Extensión de archivo — Saltar a navegación, búsqueda En informática, una extensión de archivo o extensión de fichero, es una cadena de caracteres anexada al nombre de un archivo, usualmente precedida por un punto. Su función principal es diferenciar el contenido del… …   Wikipedia Español

  • Grupo de empresas — Grupo de empresas, grupo empresarial, grupo industrial, conglomerado empresarial o conglomerado industrial es, en derecho y economía, el conglomerado de empresas que dependen todas de una misma empresa matriz, porque ésta tiene una participación… …   Wikipedia Español

  • Extensión algebraica — Saltar a navegación, búsqueda En álgebra abstracta, una extensión de cuerpo L/K se dice algebraica si cada elemento de L es algebraico sobre K, i.e. si cada elemento de L es una raíz de algún polinomio distinto de cero con coeficientes en K. Las… …   Wikipedia Español

  • Grupo Evolución Tucumán — Saltar a navegación, búsqueda Grupo Evolución Tucumán (GET) Esta formación fue una agrupación política que nació en Tucumán (Argentina) en el año 1969 y desapareció en 1973 74 tras ingresar gran parte de sus miembros en organizaciones de la… …   Wikipedia Español

  • Extensión de cuerpo — Saltar a navegación, búsqueda En Álgebra, las extensiones de cuerpo son el problema fundamental de la Teoría de Cuerpos. Un cuerpo es un conjunto en el que las operaciones suma y producto están definidas y funcionan bien . Cuando se construye una …   Wikipedia Español

  • Grupo Axé Capoeira — Date founded 1982 Country of origin Brazil Founder Mestre Barrão …   Wikipedia

  • Grupo (de la Isla) Almirante — Saltar a navegación, búsqueda Grupo (de la Isla) Almirante Distribución geográfica: Islas del Almirantazgo Países: Hablantes: {{{hablantes}}} …   Wikipedia Español

  • Grupo Castillo de Tabernas — Fundación 1993 Sede Tabernas, provincia de Almería (España) …   Wikipedia Español

  • Grupo de Galois — En matemática, un grupo de Galois es un grupo asociado a un cierto tipo de extensión de cuerpo. El estudio de las extensiones de cuerpos (y los polinomios que dan lugar a ellas) mediante el grupo de Galois es conocido como Teoría de Galois. Para… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”