Insolación

Insolación

Para la enfermedad, ver Insolación (enfermedad).

Insolación - España
Insolación media en Europa medida en superficie.

La insolación es la cantidad de energía en forma de radiación solar que llega a un lugar de la Tierra en un día concreto (insolación diurna) o en un año (insolación anual).

Puede calcularse asumiendo que no hay atmósfera o que se mide en la parte alta de la atmósfera y se denomina insolación diurna o anual no atenuada o que se mide en la superficie de la Tierra para lo cual hay que tener presente la atmósfera y que en este caso se denomina atenuada siendo su cálculo mucho más complejo.

Contenido

La radiación solar diurna no atenuada

Supongamos que no hay atmósfera y queremos calcular la insolación en un lugar de la Tierra de latitud \Pi \, un día con Declinación solar D y distancia Sol-Tierra r U.A..

La insolación será proporcional a la constante solar y ésta inversamente proporcional a r2:

I \propto K \propto \frac {K_0}{r^2} \,

Supongamos un instante t de ese día con el Sol a una altura h sobre el horizonte. El Sol está tan lejos que sus rayos son prácticamente paralelos. Si tenemos una superficie S' fija sobre la superficie de la Tierra en el plano del horizonte y queremos saber que energía del Sol llegará a ésta superficie. Sea S la superficie perpendicular al haz de luz necesario para iluminar S'. La superficie de S variará según la altura del Sol. Si h=90º entonces S=S'. Las dos superficies forman un ángulo 90-h=z la distancia cenital. Por tanto sus áreas cumplen S=S' \cdot cos (z) \, . A este fenómeno se le denomina Ley del coseno de Lambert y causa que en las regiones ecuatoriales donde los rayos solares caen más perpendiculares haga más calor que en las polares donde los rayos son muy oblicuos.

Por lo que el incremento de insolación que que llega a la superficie S' en un incremento de t vale:

\frac{\bigtriangleup I}{\bigtriangleup S' \bigtriangleup t}=K \cdot cos z=K \cdot sin h =\frac {K_0}{r^2} \cdot sin h \,

Dónde la altura del Sol cumple:

sin h=cos \Phi \cdot cos D \cdot cos H + sin \phi \cdot sin D \,

Dónde H es el ángulo horario del Sol.

Para hallar la energía total I que llega a la Tierra por unidad de área en un día habrá que hacer la suma:

I=\int_{orto}^{ocaso} K \cdot sin h \,dt =\frac {K_0}{r^2}\int_{H_1}^{H_2} sin h \,dt

La duración del día, prescindiendo de la refracción astronómica es 2 \cdot H \, comenzando el día con un ángulo horario -H \, y acabando con un ángulo horario H \, que cumple:

cos H=-tan \Phi \cdot tan D \,

Por lo que la insolación valdrá:

I=\int_{-H}^{+H} K \cdot sin h \,dt =\frac {2 \cdot K_0}{r^2}\int_{0}^{H} sin h \,dH

donde la integral es inmediata:

I=\int_{0}^{H} sin h \,dH =\int_{0}^{H}(cos \Phi \cdot cos D \cdot cos H + sin \phi \cdot sin D ) \,dH = \,
=cos \Phi \cdot cos D \cdot sin H + H \cdot sin \phi \cdot sin D

Por lo que la insolación diurna no atenuada vale:

I=\frac {2 \cdot K_0}{r^2} \cdot (cos \Phi \cdot cos D \cdot sin H + H \cdot sin \phi \cdot sin D)

Siendo

cos H=-tan \Phi \cdot tan D \,

Las unidades para calcular la insolación en ésta expresión

Si expresamos K_0 \frac {cal}{cm^2 \cdot minuto} \, y la Insolación I en langleys, el primer sumando habrá que multiplicarlo por \frac {720}{\pi} \, pues un día tiene 1440 minutos. El segundo sumando si expresamos H en grados sexagesimales habrá que mutlplicarlo por 4 ya que los grados dividido por 15 son horas y luego hay que multiplicar por 60 para pasar a minutos. Así que en plan práctico:

I=\frac {2 \cdot K_0}{r^2} \cdot (\frac {720}{\pi}\cdot cos \Phi \cdot cos D \cdot sin H + 4 \cdot H \cdot sin \phi \cdot sin D)

Siendo

K_0=1,967 \frac {cal}{cm^2 \cdot minuto} \,
cos H=-tan \Phi \cdot tan D \,
  • También se puede expresar H en radianes y multiplicar los dos sumandos por \frac {720}{\pi} \,

Otra fórmula para la Insolación diurna

Si la expresión anterior la dividimos por cos \Phi \cdot cos D \, resulta:

I=\frac {2 \cdot K_0 \cdot cos \Phi \cdot cos D}{r^2} \cdot (sin H + H \cdot tan \phi \cdot tan D) =\frac {2 \cdot K_0 \cdot cos \Phi \cdot cos D}{r^2} \cdot (sin H - H \cdot cos H)

Siendo

K_0=1,967 \frac {cal}{cm^2 \cdot minuto} \,
cos H=-tan \Phi \cdot tan D \,
  • Si expresamos H en radianes faltaría multiplicar por \frac {720}{\pi} \, para obtener la insolación en langleys.

Aplicación práctica

  • En el ecuador en el 21 de junio, la insolación es 800,87 langleys/día.

La insolación en lugares con día permanente

La expresión:

cos H=-tan \Phi \cdot tan D \,

indica el valor del arco semidiurno H en el momento del orto u ocaso y no tiene sentido en aquellos valores donde \Phi >90 -\epsilon \, donde el día es permanente o la noche es permanente (I=0 \, ).

En el primer caso H=12 h con lo que la insolación queda:

I=\frac {2 \cdot K_0}{r^2} \cdot 720 \cdot sin \Phi \cdot sin D

Siendo

K_0=1,967 \frac {cal}{cm^2 \cdot minuto} \,

Ejemplos

Calcular la insolación diurna en la parte alta de la atmósfera en el solsticio de verano el polo norte y sur.

  • El solsticio de verano en el polo norte ocurre el 21 de junio cuando la distancia entre el Sol y la Tierra es 1,0163 U.A. así que I=1090,97 langleys.
  • El solsticio de verano en el polo sur ocurre el 21 de diciembre cuando la distancia entre el Sol y la Tierra es 0,9837 U.A. así que I=1164,48 langleys.

En el solsticio de verano el polo norte recibe en la parte superior de la atmósfera más insolación que el Ecuador y en el polo sur el efecto es todavía mayor, por estar la Tierra más cerca del Sol.

Esto está reñido con la experiencia. Las temperaturas más altas no ocurren en el verano polar sino en los trópicos. A nivel de la superficie terrestre no es así y la explicación es fácil: los rayos solares durante el día permanente aparecen muy inclinados, atraviesan mucha atmósfera y son más absorbidos, además, la nieve, hielo y nubes hacen que el albedo sea mucho mayor en el polo que en las regiones ecuatoriales y una gran parte de la radiación incidente es reflejada.

Tabla y gráfica de valores de la insolación no atenuada

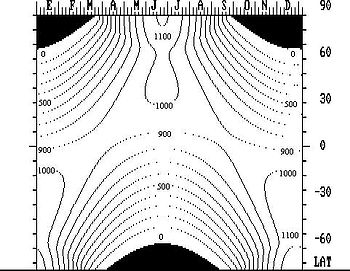El gráfico muestra la radiación solar incidente en el supuesto de ausencia de atmósfera, sobre la Tierra en función de la latitud y de la fecha. Se dibujan puntos con igual insolación diaria dada en langleys (calorias/cm2). La región oscura es la zona de insolación nula por ser noche permanente. Las curvas van de 100 en 100 langleys. Se observa que durante el verano la insolación diaria varía poco entre los polos y el ecuador en ambos hemisferios, esto es así porque en el polo la poca inclinación de los rayos solares se ve compensado por la mayor duración del día. La gráfica muestra que en verano hay más insolación en los polos que en los trópicos. En superficie esto no es así porque los rayos muy inclinados en los polos sufren mucha absorción por la atmósfera y la nieve y las nubes de las regiones polares reflejan mucha radiación (albedo) hacia el espacio.
Fecha 22 Dic. 4 Feb. 21 Mar. 6 May. 22 Jun.
Declinación Sol -26º 26' -16º 23' 0º +16º 22' +23º 26'
r (U.A.) 0,9837 0,9857 0,9960 1,0087 1,0163
La declinación solar y la distancia entre la Tierra y el Sol para unas fechas concretas

Aplicando las fórmulas anteriores se obtiene para la insolación diurna no atenuada los valores en langleys:

L a t i t u d N o r t e Ecuador L a t i t u d S u r
Fecha 90 70 50 30 0 -30 -50 -70 -90
22-dic 0,00 0,00 178,60 472,51 854,83 1054,75 1070,64 1094,25 1164,48
04-feb 0,00 24,44 292,81 576,57 890,28 987,71 922,71 797,13 822,28
21-mar 0,00 310,85 584,21 787,10 908,86 787,10 584,21 310,85 0,00
06-may 793,85 769,75 891,36 954,34 860,42 557,42 283,24 23,78 0,00
22-jun 1090,97 1025,18 1003,06 988,17 800,87 442,68 167,33 0,00 0,00

La radiación solar anual no atenuada

Para cada latitud lo único que hay que hacer es calcular la insolación diaria no atenuada y hacer la suma para todos los días del año. Distinguiremos entre el hemisferio norte y sur.

Latitud 90 º 80 º 70 º 60 º 50 º 40 º 30 º 20 º 10 º 0 º
H. Norte 129,25 133,74 148,02 178,17 214,63 248,39 276,66 297,88 311,08 315,72
H. Sur 132,33 136,77 150,91 180,83 216,98 250,36 278,17 298,90 311,62 315,72
La insolación anual no atenuada expresada en Kilolangleys = 1000 langleys

La radiación solar diurna en la superficie de la Tierra

Radiación solar atenuada en un instante dado

La radiación solar recibida por la superficie de la Tierra está atenuada, respecto a la que llega a la parte alta de la atmósfera, por distintos procesos que se producen en su recorrido por la atmósfera. Estos procesos son:

  • La difusión molecular o de Rayleigh debida a los gases atmosféricos y al vapor de agua.
  • La difusión y absorción por aerosoles o turbidez.

Vamos a suponer la ausencia de nubes, un fenómeno local que resulta imprevisible.

Los tres procesos citados atenúan la intensidad de la radiación solar cumpliendo la ley de Beer selectiva para cada longitud de onda \lambda \, . Sea un haz monocromático de intensidad I_0 (\lambda ) \, que penetra en un medio homogéneo. Tras atravesar un dl \, parte de la radiación es absorbida:

dI_0 (\lambda )=- I_0 (\lambda )\cdot K_{\lambda} \cdot \rho \cdot dl \, donde K_{\lambda} \, es el coeficiente de absorción que es una función compleja de la longitud de onda y que al tratarse de un medio gaseoso como la atmósfera depende, aparte de su composición, de la presión y la temperatura. \rho \, es la densidad de la atmósfera.

Por integración a lo largo del espesor atravesado:

I(\lambda )=I_0(\lambda ) \cdot e^ {{-\int_{0}^{l}K_{\lambda} \cdot \rho \cdot dl }}=I_0(\lambda ) \cdot e^ {{-K_{\lambda} \cdot \int_{0}^{l}\rho \cdot dl }}=I_0(\lambda ) \cdot e^ {{-K_{\lambda} \cdot m'}} \, siendo m' \,
m'=\int_{0}^{l}\rho \cdot dl la masa absorbente por unidad de superficie, contenida a lo largo del recorrido del haz.

La atenuación depende fuertemente del camino recorrido por el rayo de luz en la atmósfera y que es mínimo para una distancia cenital z=0 \, y máximo para un rayo incidiendo por el plano horizontal z=90 \, . Si el haz atraviesa un medio como la atmósfera que puede considerarse estratificado horizontalmente, esto es que el valor de sus propiedades depende exclusivamente de su altura h sobre el nivel del mar y consideramos que el rayo tiene una trayectoria recta, cumplirá:

dh=dl \cdot cos (z) \, por lo que: dl=sec (z) \cdot dh \,

Así que la insolación atenuada para un rayo con distancia cenital z vale:

I(\lambda )=I_0(\lambda ) \cdot e^ {{-K_{\lambda} \cdot \int_{h1}^{h2}\rho \cdot sec (z) \cdot dz }}=I_0(\lambda ) \cdot e^ {{-K_{\lambda} \cdot m \cdot sec (z)}} \, siendo m \,
m=\int_{h1}^{h2}\rho \cdot dh la masa absorbente por unidad de superficie, de una columna vertical de atmósfera entre las alturas h1 y h2. A esta cantidad se llama espesor óptico de la capa.


Al igual que definimos K_{\lambda} \, el coeficiente de absorción, se puede definir S_{\lambda} \, y T_{\lambda} \, como los coeficientes de difusión y turbidez, se verificará:

I(\lambda )=I_0(\lambda ) \cdot e^ {{-(K_{\lambda}+S_{\lambda}+T_{\lambda}) \cdot m \cdot sec (z)}} \,

donde m es el espesor óptico que a nivel del mar se supone que m=1, y z la distancia zenital de la radiación.

Integrando para todo el espectro electromagnético:

I=\int_0^{+\infty} I(\lambda)d \lambda=\int_0^{+\infty} I_0(\lambda ) \cdot e^ {{-K_{\lambda} \cdot sec (z)}} \cdot e^ {{-S_{\lambda} \cdot sec (z)}} e^{{-T_{\lambda} \cdot sec (z)}} d \lambda \,

En lugar de las exponenciales se pueden considerar unos factores medios a_A \, a_S \, a_T \,

así que:

I=I_0 \cdot (a_A \cdot a_S \cdot a_T)^ {sec (z)}=I_0 \cdot a^{sec (z)} \,

donde

a=a_A \cdot a_S \cdot a_T \, es producto de los valores medios de los tres coeficientes de absorción, difusión y turbidez y se toma en los cálculos un valor de a=0,7

mientras I_0=\int_0^{+\infty} I_0(\lambda ) d \lambda =\frac {K_0}{r^2} \, es la radiación solar no atenuada.

La radiación solar diurna atenuada

Supongamos un instante t del día donde queremos calcular la radiación que llega a la superficie de la Tierra, con el Sol a una altura h sobre el horizonte.

Supondremos que no hay nubes y que toda la raiación solar atenuada por los procesos descritos anteriormente llega a la superficie.

Si tenemos una superficie S' fija sobre la superficie de la Tierra en el plano del horizonte y queremos saber que energía del Sol llegará a ésta superficie. Sea S la superficie perpendicular al haz de luz necesario para iluminar S'. La superficie de S variará según la altura del Sol. Las dos superficies forman un ángulo 90-h=z la distancia cenital. Por tanto sus áreas cumplen S=S'cos z. Por lo que el incremento de insolación que que llega a la superficie S' en un incremento de t vale:

\frac{\bigtriangleup I}{\bigtriangleup S' \bigtriangleup t}=\frac {K_0}{r^2} \cdot sin h \cdot a^{sec (z)}\,

donde la altura del Sol cumple:

sin h=cos \Phi \cdot cos D \cdot cos H + sin \phi \cdot sin D \,

donde H es el ángulo horario del Sol.

Para hallar la energía total I que llega a la Tierra por unidad de área en un día habrá que hacer la suma:

I=\int_{orto}^{ocaso} \frac {K_0}{r^2} \cdot sin h \cdot a^{sec (z)} \,dt =\frac {K_0}{r^2}\int_{H_1}^{H_2} sin h \cdot a^ {\frac {1}{sin h}} \,dt

La duración del día, prescindiendo de la refracción astronómica es 2 \cdot H \, comenzando el día con un ángulo horario -H \, y acabando con un ángulo horario H \, que cumple:

cos H=-tan \Phi \cdot tan D \,

por lo que la insolación diurna atenuada valdrá:

I=\int_{-H}^{+H} \frac{K_0}{r^2} \cdot sin h \cdot a^ {\frac {1}{sin h}} \,dt =\frac {2 \cdot K_0}{r^2}\int_{0}^{H} sin h \cdot a^ {\frac {1}{sin h}} \,dH

donde supondremos a=0,7.

Para calcular la integral de forma aproximada aplicaremos el método de Simpson.

Si expresamos K_0 \frac {cal}{cm^2 \cdot minuto} \, y H en radianes, hay que multiplicar por \frac {720}{\pi} \, para que la Insolación I aparezca en langleys.

Ejemplos

  • Calcular la insolación diurna superficial el día del solsticio de verano en el polo norte cuando Ds=23,44º y r=1,0163 U.A.. Resulta una insolación de 445,0 langleys. Observar que ese día y en el polo norte la insolación no atenuada vale 1090,9 langleys por lo que sólo llega a la superficie el 40,8 % de la radiación incidente.
  • Comparar la insolación en la parte superior de la atmósfera y en la superficie a distintas latitudes el día del solsticio de verano en el hemisferio norte (21 de junio)
L a t i t u d Sur Ecuador L a t i t u d Norte
Latitud -66,5 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90
No atenuada 0 47,50 167,31 303,92 442,68 575,36 696,24 800,87 885,68 948,48 988,17 1005,15 1003,06 992,25 1025,18 1074,33 1090,97
Atenuada 0 1,19 34,50 107,25 199,05 295,62 387,47 467,79 531,61 575,39 596,88 595,15 570,85 527,03 473,59 447,92 445,00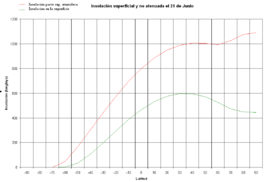
El gráfico muestra la radiación solar incidente el día del solsticio de verano en el hemisferio norte (21 de junio) en el supuesto de ausencia de atmósfera. (insolación no atenuada), y en la superficie de la Tierra (insolación atenuada) en función de la latitud. Al comparar ambas insolaciones se advierte que la insolación diaria superficial está notablemente disminuida. La mayor atenuación se produce a latitudes altas. La gráfica muestra que el 21 de junio hay más insolación en la parte superior de la atmósfera, en el polo norte que en el trópico. En superficie esto no es así porque los rayos muy inclinados en los polos sufren mucha absorción por la atmósfera y la nieve de las regiones polares reflejan mucha radiación hacia el espacio. Otro interesante efecto es que el máximo de la insolación superficial y por tanto de la temperaturas máximas superficiales, no se produce en el ecuador sino cerca del trópico. Una de las razones es que el día dura más en los trópicos que en el ecuador. El gráfico es el resultado de un programa realizado en 1995 para intentar reproducir un gráfico similar visto en el libro Meteorología de R.G. Barry y R. J. Chorley titulado Atmósfera, tiempo y clima. A partir de los datos, se ha hecho el gráfico utilizando la hoja de cálculo Excel.
El gráfico muestra la radiación solar incidente atenuada, es decir en la superficie de la Tierra en función de la latitud y de la fecha. Se dibujan puntos con igual insolación diaria dada en langleys (calorias/cm2). La región oscura es la zona de insolación nula por ser noche permanente. Las curvas van de 100 en 100 langleys. Se observan dos lóbulos de radiación solar superficial máxima en los solsticios de verano del hemisferio norte y sur y hacia una latitud de 30º norte y sur (que corresponde a los trópicos) de unos 600 langleys. Se observa que el del hemisferio sur es visiblemente mayor que el del hemisferio norte. Esto se debe a que el solsticio de verano en el hemisferio sur ocurre el 21 de diciembre cuando el Sol está más cerca de la Tierra mientras que en el hemisferio norte ocurre el 21 de junio. cuando el Sol está más alejado. Existe varios factores para que el máximo de radiación superficial se dé en los trópicos y no en el ecuador. El Sol se mueve rápido en el cenit a su paso por el ecuador y relentiza su marcha en los trópicos. El Sol está entre 6ºN y 6ºS sólo 30 días y entre 17º,5 y 23º,5 está 86 días. Además el día dura más en los trópicos que en el ecuador.

La radiación solar anual directa en la superficie de la Tierra

Para cada latitud lo único que hay que hacer es calcular la insolación diaria atenuada directa y hacer la suma para todos los días del año. Distinguiremos entre el hemisferio norte y sur.

Latitud 90 º 80 º 70 º 60 º 50 º 40 º 30 º 20 º 10 º 0 º
H. Norte 39,95 44,89 68,87 80,46 105,94 132,07 155,24 173,18 184,52 188,53
H. Sur 40,98 46,00 60,63 81,98 107,48 133,46 156,37 173,97 184,94 188,53
La insolación anual atenuada expresada en Kilolangleys = 1000 langleys

La radiación absorbida por la superficie de la Tierra

El cálculo efectuado anteriormente se refiere a la energía solar directa de onda corta que llega a la superficie de la Tierra tras sufrir los procesos de absorción y difusión por los gases de la atmósfera. Sin embargo a la superficie de la Tierra llega más energía:

  • Las nubes dispersan en promedio el 50% de la energía solar de la un 23% llega indirectamente a la Tierra como onda corta.
  • La difusión por la atmósfera disminuye la insolación directa, pero esa energía absorbida por el aire es reemitida en parte hacia la superficie de la Tierra donde es absorbida.
  • La Tierra como cuerpo caliente (en promedio a unos 15 °C) emite hacia la atmósfera una radiación de onda larga que en promedio es de unos 410 W/m2 de ella unos 40 W/m2 escapan directamente al espacio siendo el resto absorbido por los gases de efecto invernadero de la atmósfera, en promedio 361 W/m2 vuelven a la superficie terrestre en forma de onda larga calentando su superficie, este hecho se denomina efecto invernadero.

La radiación absorbida por el sistema Tierra-atmósfera

Si queremos saber la energía absorbida tanto por la Tierra como por la atmósfera habrá que sumar a la energía absorbida por la Tierra:

  • La energía solar de onda corta absorbida por el aire que en promedio representa unos 58 W/m2
  • La energía absorbida por las nubes, que es muy pequeña, del orden de 7 W/m2, ya que las nubes lo que fundamentalmente hacen es dispersar la radiación tanto hacia el espacio como hacia la Tierra.

Véase también

Enlaces externos

Bibliografía

  • Atmósfera, tiempo y clima de R.G. Barry y R.J. Chorley
  • Meteorología de Albert Miller
  • La energía radiante en la atmósfera de Emilio A. Caimi

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?
Sinónimos:
, , , ,


Mira otros diccionarios:

  • insolación — f. patol. Efecto que produce en el organismo la exposición prolongada a los rayos solares o un calor extremo. Las zonas de la piel expuestas al Sol sufren quemaduras, ampollas y erupciones; además, el sujeto se ve afectado por conjuntivitis y por …   Diccionario médico

  • insolación — sustantivo femenino 1. Trastorno producido por una exposición prolongada al sol: Está con una fuerte insolación. 2. (no contable) Área: meteorología Número de horas en que brilla el sol durante un periodo de tiempo o energía solar que recibe una… …   Diccionario Salamanca de la Lengua Española

  • insolación — 1. f. Acción y efecto de insolar. 2. Malestar o enfermedad producidos por una exposición excesiva a los rayos solares. 3. Cantidad de energía solar recibida por una superficie. 4. Meteor. Tiempo que luce el sol sin nubes …   Diccionario de la lengua española

  • insolación — {{＃}}{{LM I22127}}{{〓}} {{SynI22682}} {{［}}insolación{{］}} ‹in·so·la·ción› {{《}}▍ s.f.{{》}} {{＜}}1{{＞}} Malestar o trastorno producidos por una prolongada exposición a los rayos solares: • Tiene una insolación grave porque se durmió tomando el… …   Diccionario de uso del español actual con sinónimos y antónimos

  • insolación — ► sustantivo femenino 1 Acción y resultado de insolar o insolarse. SINÓNIMO [tabardillo] 2 MEDICINA Malestar o trastornos producidos por haberse expuesto alguien al sol durante demasiado tiempo: ■ le puso un gorrito para evitar una insolación. 3… …   Enciclopedia Universal

  • insolación — s f Enfermedad ocasionada por recibir demasiado tiempo los rayos del sol en la cabeza; se manifiesta por un estado de malestar general, dolor de cabeza, fiebre, mareos, etc: Salió de pesca y regresó con una insolación horrible …   Español en México

  • Insolación (enfermedad) — Se llama insolación, golpe de calor o infarto de calor a la enfermedad producida en la cabeza por el excesivo ardor del sol. La insolación se caracteriza por náuseas, vómitos, cefalea, calor de la piel, sopor y alteración de las fibras musculares …   Wikipedia Español

  • insolación — Radiación solar que recibe la tierra. La palabra es una contracción de Ingreso Solar por Radiación …   Diccionario ecologico

  • insolación — sustantivo femenino tabardillo (coloquial), termoplejía (medicina), acaloramiento, heliosis (medicina). * * * Sinónimos: ■ tabardillo, acaloramiento, recalentamiento, sofocación, sofocón …   Diccionario de sinónimos y antónimos

  • insolación — f. Enfermedad causada en la cabeza por el excesivo calor del sol …   Diccionario Castellano

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”