Integral y función primitiva

Integral y función primitiva

Integral y función primitiva


Integral definida es un proceso de cálculo de áreas encerradas entre una curva y un eje cartesiano.

Función Primitiva es la relación dependiente de datos sobre uno (o más) valores, que declaran los límites de un área. Es la razón del por qué se le llama función primitiva, al ser la base del cálculo integral.

Sean F y f dos funciones definidas sobre el mismo intervalo (o, más generalmente, dominio).

F es una primitiva de f si y sólo si f es la derivada de F: F' = f.

Al diferir las primitivas de una misma función f de una constante solamente, resulta que la diferencia F(b) - F(a) tiene un valor que no depende de la primitiva escogida. Es por lo tanto lógico notarla sin mencionar a F, sino solamente a f:

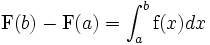
\mbox{F}(b) - \mbox{F}(a) = \int_a^b{\mbox{f}(x)dx} \,\!

Se llama integral de f entre a y b este valor. La integral tiene un significado muy concreto en el campo de la geometría: es el área entre la curva de f, el eje de los x, y dos rectas verticales x = a y x = b: éste es el teorema fundamental del análisis.

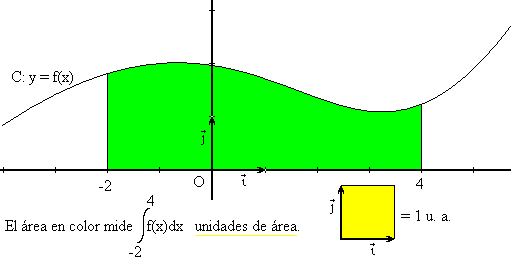
Primitiva.png

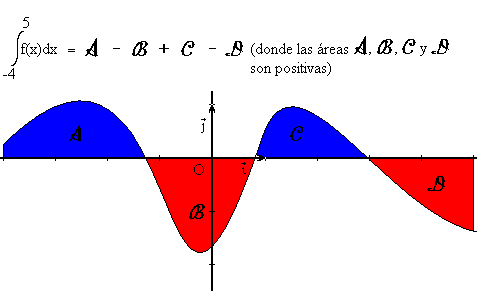
Por linealidad, cuando f es negativa en un intervalo también lo es su integral. Por lo tanto el área de la que hemos hablado es algebraica y no geométrica. Si una función es alternadamente positiva y negativa, su integral será la suma de las áreas positivas y negativas entre la curva de f y el eje de los x.

Integral alterna.png

La relación de Chasles:

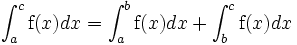
\int_a^c{\mbox{f}(x)dx} = \int_a^b{\mbox{f}(x)dx} + \int_b^c{\mbox{f}(x)dx} \,\!

cuya prueba es elemental, tanto si se recurre a argumentos geométricos (con a < b < c )como analíticos, tiene como consecuencia:

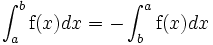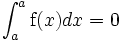
\int_a^b{\mbox{f}(x)dx} = -\int_b^a{\mbox{f}(x)dx} \,\! y \int_a^a{\mbox{f}(x)dx} = 0 \,\!

La segunda fórmula se interpreta fácilmente: el área entre las rectas x = a y .. x = a de nuevo es nula, pues la rectas están pegadas.

La primera se puede justificar así: cuando se recorre un segmento de la derecha a la izquierda, el área correspondiente cambia de signo. Esto sucede porque la noción de área está muy relacionada con el producto vectorial de dos vectores (y con el determinante), y tal producto cambia de signo si un vector lo hace.

Véase también

Fuente

El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.

.

Obtenido de "Integral y funci%C3%B3n primitiva"

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Integral y función primitiva — Integral: Proceso de cálculo de áreas. Función Primitiva: Relación dependiente de datos sobre uno (o más) valores, que declaran los límites de un área. Es la razón del por qué se le llama función primitiva, al ser la base del cálculo integral.… …   Enciclopedia Universal

  • Función — (Del lat. functio, onis.) ► sustantivo femenino 1 BIOLOGÍA Actividad o capacidad de acción específica de un ser vivo y de sus órganos: ■ la función del riñón; la función clorofílica. 2 Desempeño de un cargo u oficio: ■ el vicepresidente desempeña …   Enciclopedia Universal

  • Función trascendente — Una función trascendente es una función que no satisface una ecuación polinomial cuyos coeficientes sean a su vez polinomios; esto contrasta con las funciones algebraicas, las cuales satisfacen dicha ecuación.[1] En otras palabras, una función… …   Wikipedia Español

  • integral — (Del lat. integralis.) ► adjetivo 1 Que es global o total: ■ han hecho una reforma integral. SINÓNIMO completo 2 MATEMÁTICAS Relativo a las integrales. 3 FILOSOFÍA Se aplica a las partes no esenciales que entran en la composición de un todo.… …   Enciclopedia Universal

  • Integral impropia — En cálculo, una integral impropia es el límite de una integral definida cuando uno o ambos extremos del intervalo de integración se acercan a un número real específico, a ∞, o a −∞. Además una integral definida es impropia cuando la función… …   Wikipedia Español

  • Función gaussiana — Curvas gaussianas con distintos parámetros …   Wikipedia Español

  • Teorema fundamental del cálculo integral — Saltar a navegación, búsqueda El teorema fundamental del cálculo integral consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Esto significa que toda función continua integrable… …   Wikipedia Español

  • Introducción a la mecánica de fluidos — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Integración indefinida — El campo vectorial definido asignando a cada punto (x, y) un vector que tiene por pendiente ƒ(x) = (x3/3) (x2/2) x. Se muestran tres de las infinitas primitivas de ƒ(x) que se pueden obtener variando la constante de integración C. En cálculo… …   Wikipedia Español

  • Métodos de integración — Este artículo o sección necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso. También puedes ayudar wikificando otros artículos o cambiando este …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”