Teorema del seno

Teorema del seno
Teorema del seno.

En trigonometría, el teorema del seno es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos respectivamente opuestos.

Usualmente se presenta de la siguiente forma:

Teorema del seno

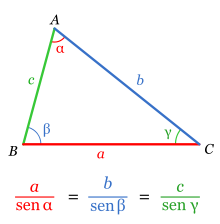
Si en un triángulo ABC, las medidas de los lados opuestos a los ángulos A, B y C son respectivamente a, b, c, entonces

\frac{a}{\operatorname{sen}\,A} =\frac{b}{\operatorname{sen}\,B} =\frac{c}{\operatorname{sen}\,C}

Contenido

Demostración

A pesar de ser de los teoremas trigonométricos más usados y de tener una demostración particularmente simple, es poco común que se presente o discuta la misma en cursos de trigonometría, de modo que es poco conocida (aunque muy elegante).

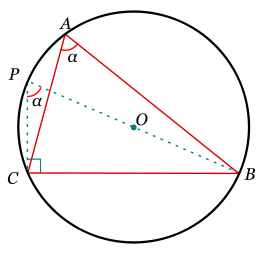
El teorema de los senos establece que a/sin(A) es constante.

Dado el triángulo ABC, denotamos por O su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento BO hasta cortar la circunferencia, se obtiene un diámetro BP.

Ahora, el triángulo PBC es recto, puesto que BP es un diámetro, y además los ángulos A y P son iguales, porque ambos son ángulos inscritos que abren el segmento BC (Véase definición de arco capaz). Por definición de la función trigonométrica seno, se tiene

\operatorname{sen}\,A=\operatorname{sen}\,P=\frac{BC}{BP} = \frac{a}{2R}

donde R es el radio de la circunferencia. Despejando 2R obtenemos:

\frac{a}{\operatorname{sen}\,A} = 2R

Repitiendo el procedimiento con un diámetro que pase por A y otro que pase por C, se llega a que las tres fracciones tienen el mismo valor 2R y por tanto son iguales.

La conclusión que se obtiene suele llamarse teorema de los senos generalizado y establece:

Para un triángulo ABC donde a, b, c son los lados opuestos a los ángulos A, B, C respectivamente, si R denota el radio de la circunferencia circunscrita, entonces:

\frac{a}{\operatorname{sen}\,A} =\frac{b}{\operatorname{sen}\,B} =\frac{c}{\operatorname{sen}\,C}=2R.

Puede enunciarse el teorema de una forma alternativa:

En un triángulo, el cociente entre cada lado y el seno de su ángulo opuesto es constante e igual al diámetro de la circunferencia circunscrita.

Aplicación

El teorema del seno es utilizado para resolver problemas en los que se conocen dos ángulos del triángulo y un lado opuesto a uno de ellos. También se usa cuando conocemos dos lados del triángulo y un ángulo opuesto a uno de ellos.

Relación con el área del triángulo

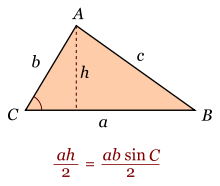
Dos fórmulas para calcular el área de un triángulo

Para un triángulo ABC, el área se calcula como ah/2 donde h es la medida de la altura sobre la base a. Nuevamente, por definición de seno, se tiene sen C = h/b o lo que es lo mismo h = b sen C, de modo que se cumple:

Area = \frac{a\;h}{2} = \frac{a\;b\,\;\operatorname{sen}\,C}{2}.

Sin embargo, el teorema de los senos implica que c = 2R sen C, por lo que al substituir en la expresión anterior se obtiene un nuevo teorema:

Area=\frac{a\;h}{2} = \frac{a\;b\,\;\operatorname{sen}\,C}{2}=\frac{a\;b\;c}{4\;R}.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Teorema del seno — Enunciado «Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos» …   Enciclopedia Universal

  • Teorema del coseno — El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos no rectángulos que se utiliza, normalmente, en trigonometría. El teorema relaciona un lado de un triángulo con los otros dos y con el coseno del ángulo formado …   Wikipedia Español

  • Teorema de la bisectriz — En este diagrama, siendo A el ángulo bisecado, BA:AC = BD:DC El teorema de la bisectriz del ángulo interno de un triángulo es un teorema de la geometría elemental la cual es una consecuencia o corolario del Teorema de Tales …   Wikipedia Español

  • Teorema de Pitágoras — El Teorema de Pitágoras establece que en un triángulo rectángulo, el área del cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de las áreas del cuadrado de los catetos (los dos lados menores del… …   Wikipedia Español

  • Teorema de la tangente — Fig. 1 Un triángulo. En trigonometría, el teorema de la tangente es una fórmula que relaciona las longitudes de los tres lados de un triángulo y las tangentes de sus ángulos. En la Figura 1, a, b, y c son las longitudes de los tres lados del… …   Wikipedia Español

  • Seno (trigonometría) — En trigonometría el seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y la Hipotenusa: O también como la ordenada correspondiente a un punto que pertenece a una circunferencia unitaria centrada en el… …   Wikipedia Español

  • Teorema de Stewart — En geometría el teorema de Stewart es una generalización del teorema de la mediana. Establece una relación entre la longitud de los lados de un triángulo y la longitud de una ceviana. Su nombre se debe al matemático escocés Matthew Stewart quién… …   Wikipedia Español

  • Teorema de Karhunen-Loève — En la teoría de procesos estocásticos, el Teorema de Karhunen Loève (así llamado debido a Kari Karhunen y Michel Loève) es una representación de un proceso estocástico como una combinación lineal infinita de funciones ortogonales. Esta… …   Wikipedia Español

  • Teorema π de Vaschy-Buckingham — El Teorema de Π (pi) de Vaschy Buckingham es el teorema fundamental del análisis dimensional. El teorema establece que dada una relación física expresable mediante una ecuación en la que están involucradas n magnitudes físicas o variables, y si… …   Wikipedia Español

  • Teorema de Fortescue — El teorema de Fortescue o teorema de las componentes simétricas es uno de los teoremas más importantes en la ingeniería eléctrica. Se utiliza para simplificar el análisis de los sistemas de energía trifásicos desequilibrados, pues permite… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”