- Anillo de fracciones
-
Anillo de fracciones
En Álgebra conmutativa son interesantes a menudo los anillo de fracciones que constituyen una generalización del concepto de cuerpo de fracciones.
Construcción del anillo de fracciones de un anillo
Sea
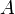 un anillo (conmutativo y unitario) y
un anillo (conmutativo y unitario) y 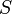 un subconjunto multiplicativamente cerrado de
un subconjunto multiplicativamente cerrado de 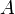 . Consideremos en
. Consideremos en 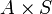 la relación binaria
la relación binaria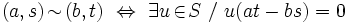
Es fácil comprobar que
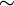 es una relación de equivalencia y, por tanto, puede considerarse el conjunto cociente
es una relación de equivalencia y, por tanto, puede considerarse el conjunto cociente 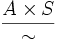 que denotaremos por
que denotaremos por 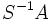 . Indicaremos por
. Indicaremos por 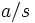 o
o 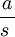 a la clase del elemento
a la clase del elemento 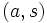 .
.
Tampoco es difícil comprobar que las operaciones adición y producto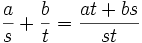
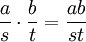
están bien definidas y dotan a
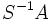 de una estructura de anillo conmutativo y unitario.
de una estructura de anillo conmutativo y unitario.
Así se ha construido el anillo de fracciones del anillo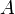 respecto de
respecto de 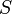 :
: 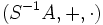 .Categoría: Teoría de anillos
.Categoría: Teoría de anillos
Wikimedia foundation. 2010.
