Cuerpo de cocientes

Cuerpo de cocientes

Cuerpo de cocientes

Una de las propiedades más interesantes de un dominio de integridad es la de que existe "el menor cuerpo que lo contiene". De forma más precisa:

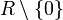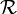Sea R un dominio íntegro (conmutativo y unitario). Denotamos por R * al conjunto R \setminus \{0\}. Establecemos en el conjunto R \times R^* la relación \mathcal{R} definida por 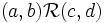(a,b) \mathcal{R} (c,d) cuando y sólo cuando 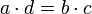a \cdot d = b \cdot c. Es sencillo comprobar que 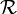\mathcal{R} es una relación de equivalencia. Denotaremos por Q(R) al conjunto cociente 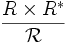\frac{R \times R^*}{\mathcal{R}}, y por 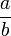\frac{a}{b} a la clase de equivalencia del elemento (a,b).

Contenido

Operaciones suma y producto en el cuerpo de cocientes.

Suma

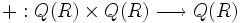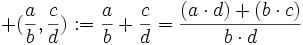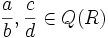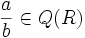Definimos la aplicación +: Q(R) \times Q(R) \longrightarrow Q(R) de la siguiente manera: + (\frac{a}{b},\frac{c}{d}) := \frac{a}{b} + \frac{c}{d} = \frac{(a \cdot d) + (b \cdot c)}{b \cdot d}, cualesquiera que sean \frac{a}{b},\frac{c}{d} \in Q(R). Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro \frac{0}{1} y que todo elemento \frac{a}{b} \in Q(R) tiene por elemento simétrico (elemento opuesto) a 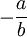- \frac{a}{b}. Así, (Q(R), + ) es un grupo abeliano.

Producto

Definimos la aplicación 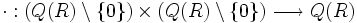\cdot: (Q(R) \setminus \{ 0 \}) \times (Q(R) \setminus \{ 0 \}) \longrightarrow Q(R) de la siguiente manera: 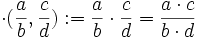\cdot (\frac{a}{b},\frac{c}{d}) := \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d}, cualesquiera que sean 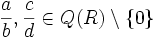\frac{a}{b},\frac{c}{d} \in Q(R) \setminus \{ 0 \}. 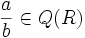Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro \frac{1}{1} y que todo elemento \frac{a}{b} \in Q(R) tiene por elemento simétrico (elemento inverso) a \frac{b}{a}. 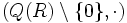Así, (Q(R) \setminus \{ 0 \},\cdot) es un grupo abeliano.

Distributividad

Se demuestra sin dificultad que \cdot es distributiva respecto de +. Esto hace que 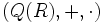(Q(R),+,\cdot) quede dotado de estructura de cuerpo.

Véase también

Obtenido de "Cuerpo de cocientes"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Cuerpo (matemática) — Saltar a navegación, búsqueda Para otros usos de este término, véase Cuerpo. Un cuerpo o campo es un anillo de división conmutativo, es decir, un anillo conmutativo en el que todo elemento distinto de cero (todo elemento no nulo) es invertible… …   Wikipedia Español

  • Dominio de integridad — Saltar a navegación, búsqueda Un dominio de integridad, dominio íntegro, anillo íntegro, o sencillamente dominio (este último término es un abuso de lenguaje y puede dar lugar a confusión, ya que la palabra dominio tiene varios usos en… …   Wikipedia Español

  • Extensión simple — Saltar a navegación, búsqueda En la teoría de cuerpos (una rama del álgebra), una extensión simple es una extensión de cuerpos L:K de manera que L está generado por un solo elemento. Contenido 1 Construcción 2 Definición de extensión simple …   Wikipedia Español

  • Elemento trascendente — Saltar a navegación, búsqueda La Teoría de Cuerpos es una rama de la Teoría de Anillos, que a su vez es una rama del Álgebra Abstracta. Uno de las principales campos de estudio de la Teoría de Cuerpos es el de decidir si un polinomio cuyos… …   Wikipedia Español

  • Número racional — En matemática, se llama número racional a todo número que puede representarse como el cociente de dos números enteros (más precisamente, un entero y un natural positivo[1] ) es decir, una fracción común a/b con numerador a y denominador distinto… …   Wikipedia Español

  • Anillo de polinomios — Saltar a navegación, búsqueda Sea A un anillo y S cualquier conjunto. El conjunto A[S] de todos los objetos (1) , en donde …   Wikipedia Español

  • Lema de Gauss — En la teoría de polinomios, el lema de Gauss, o Criterio de la irreducibilidad de Gauss, afirma que si es un dominio de factorización única (DFU) y es su cuerpo de cocientes (o cuerpo de fracciones), entonces el contenido de dos polinomios dados… …   Wikipedia Español

  • Edmontosaurus — Saltar a navegación, búsqueda ? Edmontosaurus Rango fósil: Cretácico Superior Estado d …   Wikipedia Español

  • Asamblea Parlamentaria de las Naciones Unidas — Emblema de la propuesta Asamblea Parlamentaria de las Naciones Unidas. Consiste en un fondo azul claro con el emblema en blanco, que son los colores oficiales de las Nac …   Wikipedia Español

  • Emmy Noether — Amalie Emmy Noether Nacimiento 23 de marzo de 1882 Erlangen, Baviera, Alemania Fallecimiento …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”