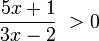En matemáticas polos y ceros es un método que permite evaluar los polos y los ceros de las expresiones racionales para hallar el conjunto solución en desigualdades. Su utilidad radica en la generalización y mecanización del proceso. Entiéndase por ceros a las expresiones polinómicas que conforman el numerador de la función y por polos a las expresiones polinómicas que conforman el denominador cuando este tiende a a cero, aproximándose la función si es evaluada al infinito.

Contenido 1 Aplicación 2 Obtención de los signos 3 Determinar si un cero o polo es par o impar 4 Véase también

Aplicación

Veamos, si queremos calcular el conjunto de solución de la siguiente inecuación

El ejemplo dado solo tiene un polo y un cero, para evaluar debemos igualar tanto numerador cero como denominador polo a cero:

cero	polo
5x + 1 = 0	3x − 2 = 0
5x = − 1	3x = 2
x = − 1 / 5	x = 2 / 3

Ahora procedemos a crear una tabla o matriz, cuya primera fila son los intervalos abiertos del conjunto de soluciones posibles de menos infinito hasta más infinito. Nótese que se usan intervalos abiertos porque la desigualdad es estricta y no incluye al cero. En la primera columna vamos a colocar el polo y el cero y vamos a evaluar en estos cada uno de los valores de los intervalos de conjunto de soluciones para ver su signo, así llenaremos el resto de la matriz, al final multiplicaremos los signos siguiendo la regla de los signos y los intervalos que cumplan con la restricción de mayores estrictos de cero conformaran la solución de la inecuación. Haciendo esto tenemos:

Obteniendo signos

x	(-∞, -1/5)	(-1/5, 2/3)	(2/3, ∞+)
(3x-2)	-	-	+
(5x+1)	-	+	+
	+	-	+

Obtención de los signos

El procedimiento correcto es evaluar de derecha a izquierda, es decir desde el infinito hasta el menos infinito, para mostrar con detalle el procedimiento vamos a hacerlo paso por paso según el ejemplo dado, el primer intervalo de posible solución a evaluar es (2/3 , ∞+) tomamos un valor que este en este intervalo y lo sustituimos en la expresión 3x − 2, tomamos por ejemplo como número aleatorio el 10 que es mayor que 2/3 pero menor que infinito (esta en el intervalo) y decimos 3 * 10 − 2 = 28 lo que arroja 28 que es un resultado positivo, escribimos "+" en la tabla, acción similar con la expresión 5x + 1 que tomando el mismo 10 tenemos 5 * 10 + 1 = 51 y 51 es un número positivo, escribimos "+" en nuestra tabla, ahora por multiplicación de signos el resultado es positivo. En la siguiente columna hacemos un procedimiento similar y tenemos que el segundo intervalo de posible solución a evaluar será (-1/5, 2/3) tomamos un valor que este en este segmento y lo sustituimos en la expresión 3x − 2, cero esta dentro del intervalo señalado y facilita el calculo, decimos 3 * 0 − 2 = − 2 lo que nos da -2 que es un número negativo, escribimos "-" en nuestra tabla, similar para la siguiente raíz 5x + 1 sustituimos x por cero, que esta el el intervalo evaluado y tenemos 5 * 0 + 1 = 1 lo que arroja un valor positivo, escribimos "+" en nuestra tabla, por multiplicación de signos tenemos, menos por más igual a menos, este intervalo es negativo. Continuamos con el último intervalo (-∞, -1/5), evaluamos para la primera raíz (3x-2) tomamos el -10 que esta en el intervalo seleccionado y al sustituir tenemos 3 * − 10 − 2 = − 32 que es un resultado negativo, escribimos "-" en nuestra tabla, la otra raíz 5x + 1 sustituimos "x" por -10 y tenemos 5 * − 10 + 1 = − 49, resultado negativo, multiplicamos signos y el intervalo es positivo. Al final la tabla nos queda como lo expuesto arriba.

También es posible analizar si el cero o el polo es par o impar y así resolver el signo de una sola columna y deducir el resto. Por ejemplo: x = 2 / 3 es un polo impar, por tanto cambia de signo de positivo a negativo en la columna de la izquierda; de la misma forma x = − 1 / 5 es un cero impar, por tanto varia el signo de negativo a positivo en la siguiente columna.

Ahora ya teniendo asignado el signo de cada raíz, identificaremos todas aquellas que cumplan con la restricción inicial, es decir mayores estrictos de cero, esto quiere decir raíces positivas. Por tanto el conjunto de solución esta dado por la unión de (-∞, -1/5) y (2/3, ∞+), cuya notación será:

 solución =  (-∞, -(1/5)) U ((2/3), ∞+)

Determinar si un cero o polo es par o impar

Esto es relativamente sencillo de hacer, si el numerador tiene esta forma por ejemplo (2x + 5)² * (3x − 5) solo se debe tomar en cuenta el exponente al que esta elevado el binomio, si es par entonces se dice que es un cero par y si es impar por consiguiente un cero impar. El mismo razonamiento es aplicable para los polos -denominador-. En este caso concreto quedaría:

2x + 5 = 0; 2x = − 5; x = − 5 / 2 cero par, ya que el exponente al que estaba elevado el binomio es par -2-.

3x − 5 = 0; 3x = 5; x = 5 / 3 cero impar, aunque no se visualice, esta tácito o sobreentendido que el exponente al que esta elevado el binomio es un 1, que es un número impar.

El conocer si un polo o cero es par o impar es de suma utilidad porque nos permite deducir sin mayores cálculos si el el signo se mantiene o varia al pasar de un intervalo de posible solución a otro. En caso de ser impar varia y si es par se mantiene.

Véase también

Inecuación

Polo (análisis complejo)

Cero (análisis complejo)