Función Lipschitz continua

Función Lipschitz continua

Función Lipschitz continua

En matemática, una función f : M → N entre espacios métricos M y N es llamada Lipschitz continua (o se dice que satisface una condición de Lipschitz) si existe una constante K > 0 tal que d(f(x), f(y)) ≤ K d(x, y) para todo x y y en M. En tal caso, K es llamada la constante Lipschitz de la función. El nombre viene del matemático alemán Rudolf Lipschitz.

Características y resultados principales

  • Toda función Lipschitz continua es uniformemente continua y por tanto continua.
  • Las funciones Lipschitz continuas con constante Lipschitz K = 1 son llamadas funciones cortas y con K < 1 reciben el nombre de contracciones. Estas últimas son las que permiten aplicar el teorema del punto fijo de Banach.
  • La condición de Lipschitz es una hipótesis importante para demostrar la existencia y unicidad de soluciones para las ecuaciones diferenciales ordinarias. La condición de continuidad de la función por sí sola nos asegura la existencia de soluciones (Teorema de Peano), pero para poder confirmar también la unicidad de la solución necesitamos también la condición de Lipschitz (Teorema de Picard-Lindelöf).
  • Si U es un subconjunto del espacio métrico M y f : U → R es una función Lipschitz continua a valores reales, entonces siempre existe una función Lipschitz continua M → R que extiende f y tiene la misma constante Lipschitz que f.(ver también teorema de Kirszbraun).
  • Una función Lipschitz continua f : I → R, donde I es un intervalo en R, es casi por todo diferenciable (siempre, excepto en un conjunto de medida de Lebesgue cero). Si K es la constante Lipschitz de f, entonces |(f')(x)| ≤ K toda vez que la derivada exista. Contrariamente, si f : I → R es una función diferenciable con derivada acotada, |(f')(x)| ≤ L para toda x en I, entonces f es Lipschitz continua con constante Lipschitz K ≤ L, una consecuencia del teorema del valor medio.

Definiciones relacionadas

Estas definiciones se requieren en el Teorema de Picard-Lindelöf y en resultados relacionados con él.

  • Localidad Lipschitz: Dados M, N, espacios métricos, se dice que una función 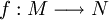f:M \longrightarrow N es localmente lipschitz si para todo punto de M existe un entorno donde la función cumple la condición Lipschitz.
  • Función Lipschitz respecto una variable: Dados M, N, L espacios métricos, se dice que una función 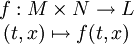\begin{matrix}f : M \times N \to L \\ (t,x) \mapsto f(t,x)\end{matrix} es localmente Lipschitz respecto x ssi cumple la condición Lipschitz para puntos de N.

Ejemplos

Sea 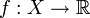f:X\rightarrow \mathbb{R} Lipchitz continua, particularizando para una función lineal del tipo f(x) = ax + b, basta tomar 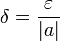\delta=\frac{\varepsilon}{|a|} y se demuestra. De paso se obtiene la continuidad uniforme.

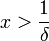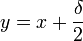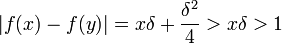En el caso de f(x) = x2, esta es Lipschitz continua pero no uniformemente continua ya que si x>\frac{1}{\delta} y y=x+\frac{\delta}{2}, entonces | x − y | < δ y |f(x)-f(y)|=x\delta+\frac{\delta^2}{4}>x\delta>1.

Obtenido de "Funci%C3%B3n Lipschitz continua"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Lipschitz continua — En matemática, una función f : M → N entre espacios métricos M y N es llamada Lipschitz continua (o se dice que satisface una condición de Lipschitz) si existe una constante K > 0 tal que d(f( …   Enciclopedia Universal

  • Función lipschitziana — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Función distancia con signo — En matemáticas la función distancia con signo mide cuan cerca se encuentra un punto x de un conjunto S otrogándole un signo según el punto se encuentre de un lado o de otro del conjunto S. donde es la distancia ordinaria de un punto a un conjunto …   Wikipedia Español

  • Dominio de Lipschitz — Saltar a navegación, búsqueda En matemática, un dominio de Lipschitz (o dominio con frontera de Lipschitz) es un dominio en el Espacio Euclidiano cuya frontera es suficientemente regular en el sentido que esta puede ser considerada como si fuera… …   Wikipedia Español

  • Continuidad uniforme — En análisis matemático una función f(x) se dice que es uniformemente continua si pequeños cambios en el valor de x producen pequeños cambios en el valor de la función (continuidad) y el tamaño de los cambios en f(x) depende solo del tamaño de los …   Wikipedia Español

  • Método de los elementos finitos — Solución de MEF en 2D para una configuración de un magnetostato, (las líneas muestran la dirección de la densidad de flujo calculada, y el color, su magnitud) …   Wikipedia Español

  • Teorema de Picard-Lindelöf — El teorema de Picard Lindelöf (muchas veces llamado simplemente teorema de Picard, otras teorema de Cauchy Lipschitz o teorema de existencia y unicidad) es un resultado matemático de gran importancia dentro del estudio de las ecuaciones… …   Wikipedia Español

  • Contracción (espacio métrico) — En matemática, una contracción o aplicación contractiva de un espacio métrico es una aplicación matemática f de un espacio métrico (M, d) en sí mismo ( ) con la propiedad de que existe un número real k < 1 tal que para todo x e y en M: El… …   Wikipedia Español

  • Espacio métrico — Saltar a navegación, búsqueda En matemática, un espacio métrico es un tipo particular de espacio topológico donde una distancia entre puntos está definida. Corresponde al caso muy común en que se dispone de una noción de distancia sobre el… …   Wikipedia Español

  • Campo vectorial — Ejemplo de campo vectorial no conservativo cuyo rotacional no se anula. En matemáticas, un campo vectorial representa la distribución espacial de una magnitud vectorial. Es una expresión de cálculo vectorial que asocia un vector a cada punto en… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”