Arco conexo

Arco conexo

Arco conexo

En topología un espacio topológico se dice que es conexo por arcos o arcoconexo si dos elementos cualesquiera pueden conectarse mediante una curva homeomorfa al intervalo unidad.

Definición

Sea 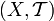(X,\mathcal{T}) un espacio topológico. Un arco en X es un embebimiento \sigma:[0,1] \longrightarrow X , es decir, una aplicación continua que es un homeomorfismo restringida a su rango \sigma:[0,1] \longrightarrow \sigma([0,1]). Obviamente se puede sustituir [0,1] por cualquier otro intervalo cerrado [a,b], ya que son todos homeomorfos.

Se dice que 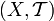(X,\mathcal{T}) es un espacio conexo por arcos o arcoconexo si para cada par de puntos distintos 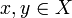x, y\in X, existe un arco σ tal que σ(0) = x y σ(1) = y.

Conexión por arcos y por caminos

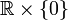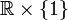Es obvio que todos los espacios conexos por arcos son conexos por caminos. El recíproco no es en general cierto. Como contraejemplo basta considerar la recta con dos orígenes: Tómense dos copias de la recta real, \mathbb{R}\times\{0\} y \mathbb{R}\times\{1\}. Definimos la recta con dos orígenes como el espacio cociente R que se obtiene al identificar (t,0) con (t,1) si 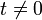t\neq0. Intuitivamente, este espacio es como la recta real, pero posee dos orígenes (las clases de (0,0) y (0,1)) que son imposibles de separar. Luego este espacio no es de Hausdorff. Más áun, no existe ningún arco que una ambos origenes. Por lo tanto R no es arcoconexo, pero es sencillo comprar que sí es conexo por caminos.

A pesar de que en general ambas nociones son distintas coinciden en una de las clases más importantes de espacios topológicos, los Hausdorff.

Obtenido de "Arco conexo"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Conjunto conexo — Un conjunto conexo es un subconjunto de un espacio topológico (donde es la colección de conjuntos abiertos del espacio topológico) que no puede ser descrito como unión disjunta de dos conjuntos abiertos de la topología. Intuitivamente, un… …   Wikipedia Español

  • Grupo fundamental — Mediante lazos con base en un punto fijo podemos explorar el espacio topológico al que pertenece. Las clases de equivalencia de estos lazos formarán el grupo fundamental. En topología, podemos asociar a cada punto p de un espacio topológico X un… …   Wikipedia Español

  • Grupo de homeotopía — En la topología el concepto de grupo de homeotopía de una superficie, S, consiste en el grupo de las clases de isotopía de los auto homeomorfismos de S donde se factorizan los auto homeomorfismos isotópicos al mapeo identidad de S. Este concepto… …   Wikipedia Español

  • Topología — Para otros usos de este término, véase Topología (desambiguación). Ilustración del Teor …   Wikipedia Español

  • Glosario en teoría de grafos — Anexo:Glosario en teoría de grafos Saltar a navegación, búsqueda Grafo con 6 nodos A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal …   Wikipedia Español

  • Anexo:Glosario de teoría de grafos — Grafo simple no dirigido, con 6 vértices y 7 aristas. A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal correspondiente. Todos los… …   Wikipedia Español

  • Algoritmo de Prim — El algoritmo de Prim es un algoritmo perteneciente a la teoría de los grafos para encontrar un árbol recubridor mínimo en un grafo conexo, no dirigido y cuyas aristas están etiquetadas. En otras palabras, el algoritmo encuentra un subconjunto de… …   Wikipedia Español

  • Ciclo euleriano — Un ciclo euleriano es aquel camino que recorre todas las aristas de un grafo pasando una y sólo una vez por cada arco (arista) del grafo, siendo condición necesaria que regrese al vértice inicial de salida (ciclo = camino en un grafo donde… …   Wikipedia Español

  • Algoritmo de Kruskal — El algoritmo de Kruskal es un algoritmo de la teoría de grafos para encontrar un árbol recubridor mínimo en un grafo conexo y ponderado. Es decir, busca un subconjunto de aristas que, formando un árbol, incluyen todos los vértices y donde el… …   Wikipedia Español

  • Cobertura de vértices — En matemáticas, en el campo de la teoría de grafos, un covering de un grafo es un conjunto de vértices (o arcos) cuyos elementos son cerrados (adyacentes) a todos los vértices (o nodos) del grafo. Es de especial interés encontrar pequeños… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”