Serie de potencias formal

Serie de potencias formal: Serie de potencias formal

Saltar a navegación, búsqueda

En matemática, se llama serie de potencias formal a una expresión matemática que extiende las propiedades de las series de potencias en cuerpos como el de los reales o el de los complejos, permitiendo dar sentido formal a diversas notaciones que técnicamente carecen de rigurosidad. Las series formales de potencias tienen diversas aplicaciones, pudiéndose mencionar la combinatoria y la teoría de números.

Definición

Informalmente podemos pensar que una serie de potencias formal es una serie infinita de términos de la forma

$S(x) = \sum_{k=0}^{\infty} a_k x^k$

esto es, un polinomio con infinitos términos, en que los a_k son elementos de un cuerpo. Para formalizar esto, consideremos el conjunto de todas las sucesiones infinitas de elementos de un cuerpo 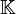$\mathbb{K}$ , las cuales representaremos de esta forma: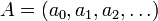

$A = (a_0,a_1,a_2,\dots)$

Denotaremos al conjunto de todas estas sucesiones con el símbolo $\mathbb{K}^\infty$ . Definimos la suma de estas sucesiones de la siguiente forma:

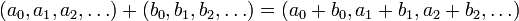
$(a_0,a_1,a_2,\dots) + (b_0,b_1,b_2,\dots) = (a_0+b_0,a_1+b_1,a_2+b_2,\dots)$

y su ponderación (multiplicación por escalar) por un elemento del cuerpo 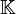$\mathbb{K}$ como:

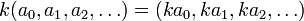
$k(a_0,a_1,a_2,\dots) = (ka_0,ka_1,ka_2,\dots)$

Esto le da al conjunto $\mathbb{K}^\infty$ una estructura de espacio vectorial sobre $\mathbb{K}$ , como puede comprobarse directamente. Ahora definimos el producto entre dos sucesiones de $\mathbb{K}^\infty$ según la fórmula:

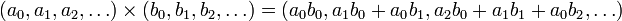
$(a_0,a_1,a_2,\dots) \times (b_0,b_1,b_2,\dots) = (a_0b_0,a_1b_0+a_0b_1,a_2b_0+a_1b_1+a_0b_2,\dots)$

en que, si $A \times B = C = (c_0,c_1,c_2,\dots)$ , el término general c_k es:

c_k = ∑ a_mb_n

m + n = k

Nótese que esta definición coincide con la de producto de Cauchy de dos sucesiones. Asimismo, si multiplicamos dos polinomios (o dos series absolutamente convergentes) con coeficientes reales o complejos, vemos que los coeficientes del resultado siguen una regla análoga. Por lo mismo esta definición es coherente desde un punto de vista intuitivo.

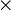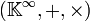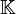Se puede demostrar por la definición que la operación $\times$ en $\mathbb{K}^\infty$ es conmutativa, asociativa y distributiva, lo que implica que $(\mathbb{K}^\infty, +, \times)$ es una $\mathbb{K}$ -álgebra lineal conmutativa con unidad, es decir, una estructura algebraica que es tanto espacio vectorial como anillo conmutativo con unidad, siendo el elemento neutro la sucesión 1 = (1,0,0,...).

Adoptaremos, como es habitual, la notación 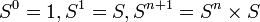$S^0 = 1, S^1 = S, S^{n+1} = S^n \times S$ . Denotaremos por x a la sucesión (0,1,0,0,...). Nótese que en el resto de este artículo la letra x denotará a dicha sucesión y no a una variable. Tenemos entonces:

$x 0 = (1,0,0,0,...), x 1 = (0,1,0,0,...), x 2 = (0,0,1,0,...), x 3 = (0,0,0,1,...)$

etc. Tenemos entonces la igualdad:

$(a_0,a_1,a_2,a_3,\dots) = a_0 x^0 + a_1 x^1 + a_2 x^2 + a_3 x^3 + \dots = \sum_{k=0}^{\infty} a_k x^k$

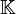Esta es la definición de una serie formal de potencias. Nótese que el conjunto de las series de potencias para los cuales existe un índice k que satisface que a_n = 0 para todo n > k es una sub-álgebra lineal de $\mathbb{K}^\infty$ isomorfa al conjunto de las funciones polinomios en el cuerpo $\mathbb{K}$ (a menos que dicho cuerpo sea finito). En general, denotamos a ambos conjuntos con el símbolo $\mathbb{K}[x]$ y no hacemos distinción entre una serie formal finita y un polinomio.

Nótese que en el concepto de serie formal de potencias la notación 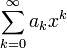$\sum_{k=0}^{\infty} a_k x^k$ es solamente una expresión conveniente y no alude en ninguna forma a la convergencia o divergencia de la serie, o a asignarle un valor. Se reitera que x representa a la sucesión (0,1,0,0...) y no es una variable. En el caso de una serie finita (polinomio) existe una forma de asignarle directamente un valor, lo que se analizará posteriormente.^[1]

Asignación de un valor a una serie de potencias formal

A pesar de que el trabajo con una serie de potencias formal no involucra de ninguna forma el asignarle un valor a una serie $S = S(x) = (a_0,a_1,a_2,\dots) = a_0x^0 + a_1x^1 + a_2x^2 + \dots$ , podemos, si es conveniente, asignar en ciertos casos un número a una serie de potencias S, de la siguiente forma:

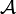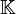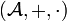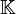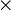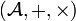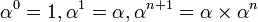Sea $\mathcal{A}$ una $\mathbb{K}$ -álgebra lineal con unidad, i.e. un espacio vectorial $(\mathcal{A},+,\cdot)$ sobre $\mathbb{K}$ con una segunda operación $\times$ que le da a $(\mathcal{A},+,\times)$ una estructura de anillo con unidad. Como antes, dado un elemento $\alpha \in \mathcal{A}$ , denotamos $\alpha^0 = 1, \alpha^1 = \alpha, \alpha^{n+1} = \alpha \times \alpha^n$ , en que 1 es el elemento unidad de 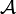$\mathcal{A}$ (como es usual). 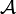Entonces, dada una serie finita o polinomio formal $S(x) = (s_0x^0 + s_1x^1 + s_2x^2 + \dots + s_nx^n) \in \mathbb{K}[x]$ , se le asigna a cada $\alpha \in \mathcal{A}$ un elemento de $\mathcal{A}$ dado por:

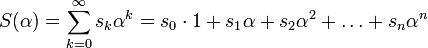
$S(\alpha) = \sum_{k=0}^{\infty} s_k\alpha^k = s_0 \cdot 1 + s_1\alpha + s_2\alpha^2 + \dots + s_n\alpha^n$

Por ejemplo, si $P(x) = (1 + x^2 - 3x^4) \in \mathbb{R}[x]$ , se tiene que $P (2) = (1 + (2) 2 - 3((2) 4)) = 1 + 4 - 48 = - 43$ .

Para asignar de una forma análoga un valor a una serie de potencias formal infinita se deben introducir los conceptos de límite y convergencia, para lo cual es necesario definir una topología sobre el conjunto 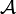$\mathcal{A}$ . Por ejemplo, si consideramos la serie 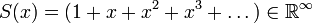$S(x) = (1 + x + x^2 + x^3 + \dots) \in \mathbb{R}^\infty$ , podemos decir, por ejemplo, que: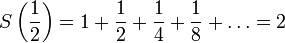

$S\left(\frac{1}{2}\right) = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots = 2$

y, en general:

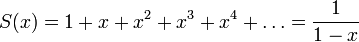
$S(x) = 1 + x + x^2 + x^3 + x^4 + \dots = \frac{1}{1-x}$

Sin embargo, por la forma en que se ha construido la topología de $\mathbb{R}$ , esto es, por la definición de límite en el cuerpo de los reales, la última igualdad es válida solamente cuando |x| < 1. Sin embargo, mediante manipulaciones algebraicas o analíticas puede asignársele un valor a otras series a pesar de que no converjan en sentido estricto (véase Serie divergente para más detalles), por ejemplo, dada la misma serie del ejemplo anterior, intentemos asignar mediante métodos del álgebra un valor a S(2):

S(2) = 1 + 2 + 4 + 8 + ... = u

2u = 2·1 + 2·2 + 2·4 + 2·8 + ... = 2 + 4 + 8 + 16 + ... = (1 + 2 + 4 + 8 + 16 + ...) - 1 = u - 1

2u = u - 1

u = -1

Podemos ver que, a pesar de que esto en sentido estricto no es correcto, es un resultado coherente y podemos considerarlo válido en cierto contexto en que se requiera que S(2) tenga un valor.

Referencias

↑ Kenneth Hoffman, Ray Kunze, Álgebra lineal. Editorial Prentice-Hall Internacional.

Obtenido de "Serie de potencias formal"

Categorías: Álgebra | Análisis matemático

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

Serie formal de potencias — En matemática, se llama serie formal de potencias (a veces serie de potencias formal) a una expresión matemática que extiende las propiedades de las series de potencias en cuerpos como el de los reales o el de los complejos, permitiendo dar… … Wikipedia Español
Serie de Bell — En matemática, una serie de Bell es una serie de potencias formal utilizada para estudiar la propiedades de funciones aritméticas. Las series de Bell fueron introducidas y desarrolladas por Eric Temple Bell. Dada una función aritmética f y un… … Wikipedia Español
Potencias del Eje en la Segunda Guerra Mundial — Mapamundi con los participantes en la Segunda Guerra Mundial. Aliados Aliados tras el ataqu … Wikipedia Español
Serie convergente — En matemáticas, una serie se llama serie convergente si la sucesión de sumas parciales tiene un límite en el espacio considerado. De otro modo se llama serie divergente. Contenido 1 Definición formal 2 Ejemplos 3 Convergencia absoluta … Wikipedia Español
Álgebra de incidencia — Un conjunto parcialmente ordenado es localmente finito cuando cada intervalo cerrado [a, b] es finito. Para cada poset localmente finito y cada cuerpo de escalares hay un álgebra de incidencia, que es un álgebra asociativa definida como sigue.… … Wikipedia Español
Teorema de Cauchy-Hadamard — En matemática, el Teorema de Cauchy Hadamard, llamado así por los matemáticos franceses Augustin Louis Cauchy y Jacques Hadamard, estableciendo el radio de convergencia de una serie de potencias que aproxima una función en torno de un punto a.… … Wikipedia Español
Teorema del número pentagonal — En matemáticas, el teorema del número pentagonal, originalmente formulado por Leonhard Euler, da una equivalencia entre la representación en forma producto y de serie de la función de Euler. Se formula como: Leonhard Euler (1775) … Wikipedia Español
Símbolo q-Pochhammer — En matemáticas, en el área de combinatoria, el símbolo q Pochhmammer es el q análogo del más conocido símbolo de Pochhammer. Se define de la siguiente manera: El símbolo q Pochhmammer es el más importante ladrillo en la construcción de los q… … Wikipedia Español
Anillo local — Saltar a navegación, búsqueda En Álgebra abstracta, los anillos locales son ciertos anillos comparativamente simples y que sirven para describir el comportamiento local de las funciones definidas sobre variedades algebraicas o variedades… … Wikipedia Español
Función zeta de Artin-Mazur — En matemáticas, la función zeta de Artin Mazur es una herramienta para el estudio de las funciones iteradas que aparecen en los sistemas dinámicos y fractales. La misma es definida como la serie de potencias formal , donde Fix(fn) es el conjunto… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Serie de potencias formal

Serie de potencias formal

Definición

Asignación de un valor a una serie de potencias formal

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

c_k =	∑	a_mb_n
	m + n = k

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Serie de potencias formal

Serie de potencias formal

Definición

Asignación de un valor a una serie de potencias formal

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo