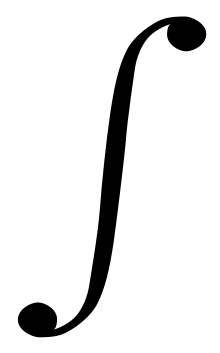- Signo de integración
-
El símbolo ∫ se usa para denotar una integral en matemáticas. La notacion fue introducida por el matemático y filósofo alemán Gottfried Lebnitz a finales del siglo XVII. El símbolo se basó en el carácter ſ (S larga), y se escogió debido a que una integral es el límite de una suma.
El Símbolo ∫ es U+222B en Unicode,
\inten LaTeX. En HTML, se escribe∫en (hexadecimal),∫(decimal) y∫.El paquete de caracteres de la página de código 437 de IBM PC original tenía un par de caracteres ⌠ y ⌡ (códigos 244 y 245, respectivamente) para construir el símbolo. Estos fueron remplazados en las subsecuentes páginas de código de MS-DOS, pero siguen existiendo en Unicode (U+2320 y U+2321, respectivamente) por compatibilidad.
El símbolo ∫ es bastante similar, pero no debe confundirse con símbolo (ʃ) llamado esh.
Símbolos relacionados son ∬ (integral doble, U+222C), ∭ (integral triple, U+222D), ∮ (integral de contorno, U+222E), ∯ (integral de superficie, U+222F), y ∰ (integral de volumen, U+2230).
Referencias
- Stewart, James (2003). «Integrals». Single Variable Calculus: Early Transcendentals (5th edition edición). Belmont, CA: Brooks/Cole. pp. 381. ISBN 0-534-39330-6.
Enlaces externos
Wikimedia foundation. 2010.