- Símbolos matemáticos
-
Anexo:Símbolos matemáticos
Genéricos
Símbolo Nombre se lee como Categoría =
igualdad igual a todos x = y significa: x y y son nombres diferentes que hacen referencia a un mismo objeto o ente. 1 + 2 = 6 − 3 ≔
≡
:⇔definición se define como todos x := y o x ≡ y significa: x se define como otro nombre para y (notar, sin embargo, que ≡ puede también significar otras cosas, como congruencia)
P :⇔ Q significa: P se define como lógicamente equivalente a Qcosh x := (1/2)(exp x + exp (−x)); A XOR B :⇔ (A 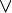 B)
B) 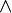 ¬(A
¬(A 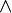 B)
B)Aritmética
Símbolo Nombre se lee como Categoría +
adición más aritmética 4 + 6 = 10 significa que si a cuatro se le agrega 6, la suma, o resultado, es 10. 43 + 65 = 108; 2 + 7 = 9 −
substracción menos aritmética 9 − 4 = 5 significa que si 4 es restado de 9, el resultado será 5. El símbolo 'menos' también se utiliza para denotar que un número es negativo. Por ejemplo, 5 + (−3) = 2 significa que si 'cinco' y 'menos tres' son sumados, el resultado es 'dos'. 87 − 36 = 51 ×
·
*multiplicación por aritmética 7 x 6 = 42 significa que si se cuenta siete veces seis, el resultado será 42. 4 x 6 = 24 ó 4 * 6 = 24 ó 4 · 6 = 24 ÷
/
:división entre aritmética 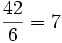 significa que si se hace seis pedazos uniformes de cuarenta y dos, cada pedazo será de tamaño siete.
significa que si se hace seis pedazos uniformes de cuarenta y dos, cada pedazo será de tamaño siete.24 / 6 = 4 ∑
sumatoria suma sobre ... desde ... hasta ... de aritmética ∑k=1n ak significa: a1 + a2 + ... + an ∑k=14 k² = 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16 = 30 ∏
productorio producto sobre... desde ... hasta ... de aritmética ∏k=1n ak significa: a1a2···an ∏k=14 (k + 2) = (1 + 2)(2 + 2)(3 + 2)(4 + 2) = 3 × 4 × 5 × 6 = 360 Lógica proposicional
Símbolo Nombre se lee como Categoría ⇒
→implicación material o en un solo sentido implica; si .. entonces; por lo tanto lógica proposicional A ⇒ B significa: si A es verdadero entonces B es verdadero también; si B es verdadero entonces nada se dice sobre A.
→ puede significar lo mismo que ⇒, o puede ser usado para denotar funciones, como se indica más abajo.x = 2 ⇒ x² = 4 es verdadera, pero 4 = x² ⇒ x = 2 es, en general, falso (ya que x podría ser −2)
/ tal que ejemplo x/y se lee x tal que y⇔
↔doble implicación si y sólo si; sii[1] lógica proposicional A ⇔ B significa: A es verdadera si B es verdadera y A es falsa si B es falsa. x + 5 = y + 2 ⇔ x + 3 = y ∧
conjunción lógica o intersección en una reja y lógica proposicional, teoría de rejas la proposición A ∧ B es verdadera si A y B son ambas verdaderas; de otra manera es falsa.todo es verdadero de los valores n < 4 ∧ n > 2 ⇔ n = 3 cuando n es un número natural ∨
disyunción lógica o unión en una reja o lógica proposicional, teoría de rejas la proposición A ∨ B es verdadera si A o B (o ambas) son verdaderas; si ambas son falsas, la proposición es falsa. n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 cuando n es un número natural ¬
/negación lógica no lógica proposicional la proposición ¬A es verdadera si y sólo si A es falsa.
una barra colocada sobre otro operador es equivalente a un ¬ colocado a la izquierda.¬(A ∧ B) ⇔ (¬A) ∨ (¬B); x ∉ S ⇔ ¬(x ∈ S) Lógica de predicados
Símbolo Nombre se lee como Categoría ∀
cuantificador universal para todos; para cualquier; para cada lógica de predicados ∀ x: P(x) significa: P(x) es verdadera para cualquier x ∀ n ∈ N: n² ≥ n ∃
cuantificador existencial existe por lo menos un/os lógica de predicados ∃ x: P(x) significa: existe por lo menos un x tal que P(x) es verdadera. ∃ n ∈ N: n + 5 = 2n ∃!
cuantificador existencial con marca de unicidad existe un/os único/s lógica de predicados ∃! x: P(x) significa: existe un único x tal que P(x) es verdadera. ∃! n ∈ N: n + 1 = 2 :
reluz tal que lógica de predicados ∃ x: P(x) significa: existe por lo menos un x tal que P(x) es verdadera. ∃ n ∈ N: n + 5 = 2n Teoría de conjuntos
Símbolo Nombre se lee como Categoría { , }
delimitadores de conjunto el conjunto de ... teoría de conjuntos {a,b,c} significa: el conjunto consistente de a, b, y c N = {0,1,2,...} { : }
{ | }notación constructora de conjuntos el conjunto de los elementos ... tales que ... teoría de conjuntos {x : P(x)} significa: el conjunto de todos los x para los cuales P(x) es verdadera. {x | P(x)} es lo mismo que {x : P(x)}. {n ∈ N : n² < 20} = {0,1,2,3,4} ∅
{}conjunto vacío conjunto vacío teoría de conjuntos {} significa: el conjunto que no tiene elementos; ∅ es la misma cosa. {n ∈ N : 1 < n² < 4} = {} ∈
∉pertenencia de conjuntos en; está en; es elemento de; es miembro de; pertenece a teoría de conjuntos a ∈ S significa: a es elemento del conjunto S; a ∉ S significa: a no es elemento del conjunto S (1/2)−1 ∈ N; 2−1 ∉ N ⊆
⊂subconjunto es subconjunto de teoría de conjuntos A ⊆ B significa: cada elemento de A es también elemento de B
A ⊂ B significa: A ⊆ B pero A ≠ BA ∩ B ⊆ A; Q ⊂ R ∪
unión conjunto-teorética la unión de ... y ...; unión teoría de conjuntos A ∪ B significa: el conjunto que contiene todos los elementos de A y también todos aquellos de B, pero ningún otro. A ⊆ B ⇔ A ∪ B = B ∩
intersección conjunto-teorética la intersección de ... y ...; intersección teoría de conjuntos A ∩ B significa: el conjunto que contiene todos aquellos elementos que A y B tienen en común. {x ∈ R : x² = 1} ∩ N = {1} \
complemento conjunto-teorético menos; sin teoría de conjuntos A \ B significa: el conjunto que contiene todos aquellos elementos de A que no se encuentran en B {1,2,3,4} \ {3,4,5,6} = {1,2} Funciones
Símbolo Nombre se lee como Categoría ( )
[ ]
{ }aplicación de función; agrupamiento de funciones para aplicación de función: f(x) significa: el valor de la función f sobre el elemento x
para agrupamiento: realizar primero las operaciones dentro del paréntesis.Si f(x) := x², entonces f(3) = 3² = 9; (8/4)/2 = 2/2 = 1, pero 8/(4/2) = 8/2 = 4 f:X→Y
mapeo funcional de ... a funciones f: X → Y significa: la función f mapea el conjunto X al conjunto Y Considérese la función f: Z → N definida por f(x) = x² Números
Símbolo Nombre se lee como Categoría N
números naturales N números N significa: {0,1,2,3,...}, pero véase el artículo números naturales para una convención diferente. {|a| : a ∈ Z} = N Z
números enteros Z números Z significa: {...,−3,−2,−1,0,1,2,3,4,...} {a : |a| ∈ N} = Z Q
números racionales Q números Q significa: {p/q : p, q ∈ Z, q ≠ 0} 3.14 ∈ Q; π ∉ Q R
números reales R números R significa: {limn→∞ an : ∀ n ∈ N: an ∈ Q, el límite existe} π ∈ R; √(−1) ∉ R C
números complejos C números C significa: {a + bi : a, b ∈ R} i = √(−1) ∈ C √
raíz cuadrada la raíz cuadrada de; la principal raíz cuadrada de números reales √x significa: el número positivo cuyo cuadrado es x √(x²) = |x| ∞
infinito infinito números ∞ es un elemento de la línea extendida de números reales mayor que todos los números reales; ocurre frecuentemente en límites limx→0 1/|x| = ∞ | |
valor absoluto valor absoluto de números |x| significa: la distancia en la línea real (o en el plano complejo) entre x y zero |a + bi | = √(a² + b²) Órdenes parciales
Símbolo Nombre se lee como Categoría ≤
≥comparación es menor o igual a, es mayor o igual a órdenes parciales x ≤ y significa: x es menor o igual a y; x ≥ y significa: x es mayor o igual a y x ≥ 1 ⇒ x² ≥ x Geometría euclídea
Símbolo Nombre se lee como Categoría π
pi pi Geometría euclideana π significa: la razón de la circunferencia a su diámetro. A = πr² es el área de un círculo con radio r Combinatoria
Símbolo Nombre se lee como Categoría !
factorial factorial combinatoria n! es el producto 1×2×...×n 4! = 24 Análisis funcional
Símbolo Nombre se lee como Categoría || ||
norma norma de; longitud de análisis funcional ||x|| es la norma del elemento x de un espacio vectorial normado ||x+y|| ≤ ||x|| + ||y|| Cálculo
Símbolo Nombre se lee como Categoría ∫
integración integral desde ... hasta ... de ... con respecto a ... cálculo ∫ab f(x) dx significa: el área, con signo, entre el eje-x y la gráfica de la función f entre x = a y x = b ∫0b x² dx = b³/3; ∫x² dx = x³/3 f '
derivación derivada de f; f prima cálculo f '(x) es la derivada de la función f en el punto x, esto es, la pendiente de la tangente en ese lugar. Si f(x) = x², entonces f '(x) = 2x y f ' '(x) = 2 ∇
gradiente del, nabla, gradiente de cálculo ∇f (x1, …, xn) es el vector de derivadas parciales (df / dx1, …, df / dxn) Si f (x, y, z) = 3xy + z² entonces ∇f = (3y, 3x, 2z) ∂
derivación parcial derivada parcial de cálculo Con f (x1, …, xn), ∂f/∂xi es la derivada de f con respecto a xi, con todas las otras variables mantenidas constantes. Si f(x, y) = x²y, entonces ∂f/∂x = 2xy Ortogonalidad
Símbolo Nombre se lee como Categoría ⊥
perpendicular es perpendicular a ortogonalidad x ⊥ y significa: x es perpendicular a y; o, más generalmente, x es ortogonal a y. Álgebra matricial
Símbolo Nombre se lee como Categoría ⊥
perpendicular traspuesta matrices y vectores (a,b) con ⊥ al lado o a modo de potencia significa que el vector se debe colocar no de izquierda a derecha, sino de arriba a abajo. En numerosos trabajos de investigación se utiliza esta sintaxis al no poder representar en un documento vectores verticales. Teoría de rejas
Símbolo Nombre se lee como Categoría ⊥
fondo el elemento fondo teoría de rejas x = ⊥ significa: x es el elemento más pequeño. Véase también
wikipedia: Cómo se edita una página contiene información acerca de cómo producir símbolos matemáticos en otros artículos.
Referencias
- ↑ sii es usado por los matemáticos como jerga ocasional, no está reconocido como un término estándar, por lo que tampoco suele aparecer en textos formales.
''Este artículo utiliza [[Tabla de símbolos matemáticos|símbolos matemáticos]]''
Enlaces externos
- Jeff Miller: Earliest Uses de Various Mathematical Symbols, http://members.aol.com/jeff570/mathsym.html
- TCAEP - Institute of Physics, http://www.tcaep.co.uk/science/symbols/maths.htm
Categorías: Anexos:Matemáticas | Símbolos matemáticos
Wikimedia foundation. 2010.
