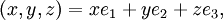En álgebra lineal, una base ortonormal de un espacio prehilbertiano V (es decir, un espacio vectorial con producto interno) o, en particular, de un espacio de Hilbert H, es un conjunto de elementos cuyo span es denso en el espacio, en el que los elementos son mutuamente ortogonales y normales, es decir, de magnitud unitaria. Una base ortogonal satisface las mismas condiciones, salvo la de magnitud unitaria; es muy sencillo transformar una base ortogonal en una base ortonormal mediante el producto por un escalar apropiado y de hecho, esta es la forma habitual en la que se obtiene una base ortonormal: por medio de una base ortogonal.

Así, una base ortonormal es una base ortogonal, en la cual la norma de cada elemento que la compone es unitaria.

Estos conceptos son importantes tanto para espacios de dimensión finita como de dimensión infinita. Para espacios de dimensión finita, la condición de span denso es la misma que la de 'span', como se usa en álgebra lineal.

Una base ortonormal por lo general no es una "base", es decir, en general no es posible escribir a cada elemento del espacio como una combinación lineal de un número finito de elementos de la base ortonormal. En el caso de dimensión infinita, esta distinción cobra importancia: la definición dada requiere solo que el span de una base ortonormal sea densa en el espacio vectorial, y no que iguale al espacio entero.

Una base ortonormal de un espacio vectorial V no tiene sentido si el espacio no posee un producto interno. Un Espacio de Banach no tendrá una base ortonormal a no ser que sea un espacio de Hilbert.

Ejemplos

• El conjunto {e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1)} (la base estándar) forma una base ortonormal de R³.

Demostración: Mediante un cálculo directo se verifica que 〈e₁, e₂〉 = 〈e₁, e₃〉 = 〈e₂, e₃〉 = 0 y que ||e₁|| = ||e₂|| = ||e₃|| = 1. Así, {e₁, e₂, e₃} es un conjunto ortonormal. Para un (x,y,z) cualquiera en R³ tenemos

entonces, {e₁,e₂,e₃} reconstruye R³ y por lo tanto tiene que ser una base. También puede demostrarse que la base estándar rotada alrededor de un eje que pasa por el origen o reflejada en un plano que pasa por el origen forma también una base ortonormal de R³.

• El conjunto {f_n : n ∈ Z} con f_n(x) = exp(2πinx) forma una base ortogonal del espacio complejo L²([0,1]). Este es un resultado fundamental para el estudio de series de Fourier.
• El conjunto {e_b : b ∈ B} con e_b(c) = 1 si b=c y 0 en caso contrario forma una base ortonormal de l²(B).
• Eigenfunciones de un Eigenproblema de Sturm-Liouville.

Construcción

Al igual que con una base ortogonal, se puede crear un arreglo de bases ortonormales para formar una matriz ortonormal.

Para poder construir una base ortonormal de una base cualquiera es necesario primero ortogonalizar a la base para luego ortonormalizarla. Existe el método de ortonormalización de Gram-Schmidt con el cual es posible realizar lo anterior.