- Bola (matemática)
-
Bola (matemática)
Una bola, en topología y otras ramas de matemática, es el conjunto de puntos que distan de otro igual o menos que una distancia dada, llamada radio. Es un concepto fundamental en el Análisis Matemático. Se distinguen dos tipos: las abiertas y las cerradas.
Contenido
Bola abierta
Una bola abierta, en topología, es el conjunto de puntos que distan de otro punto (el centro), una distancia menor a la determinada (el radio). Equivale al conjunto de puntos contenidos dento de una superficie esférica, excluida dicha superficie.
Definición y notaciones
Sea (E,d) un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que d sea pseudodistancia). Sea un número real r > 0. Sea
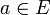. Se define la bola abierta de centro a y radio r (o simplemente bola de centro a y radio r) como el conjunto 
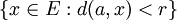.Este conjunto tiene distintas maneras de denotarse. La usual y universal es B(a,r). A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación: Bd(a,r). En algunos textos se denota sin embargo por Br(a).
En Análisis Funcional, cuando se trabaja con espacios normados se prefiere la notación U(a,r) para denotar la bola abierta. Así, U denota a la bola de centro 0 y radio 1. La notación B(a,r) se reserva para las bolas cerradas (con el peligro de confusión que eso genera).
Cuando hablamos de espacios euclídeos, la bola es "redonda", en el sentido intuitivo del término, por lo que la bola de centro a y radio r coincide en esos casos con los puntos encerrados en el interior de una superficie esférica. En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto
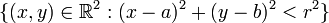) es el disco (abierto) de centro (a,b) y radio r, razón por la cual se denota por Δ((a,b),r). Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación 
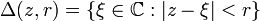(donde | ξ | representa el módulo de ξ). Aunque no es estándar, sí es usual encontrar textos en los que Δ denota al disco de radio unidad centrado en el origen, i.e., Δ = B(0,1).Propiedades
Toda bola abierta es un conjunto abierto.
El conjunto de todas las bolas abiertas de un espacio pseudométrico (
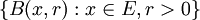) forman una base de la topología asociada a la pseudodistancia. Si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto x), el conjunto de bolas abiertas centradas en x ({B(x,r):r > 0}) forman una base de entornos de x. En concreto es una base de entornos abiertos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos: 
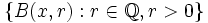que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio pseudométrico cumple el Primer Axioma de Numerabilidad.Si el espacio es un espacio normado, toda bola abierta es homeomorfa al espacio.
En matemática (en concreto en topología y en las ramas que la utilizan), una bola cerrada es un conjunto de puntos que distan de otro no más que un cierto radio. Es un concepto fundamental en el Análisis Matemático.
Bola cerrada
Una bola cerrada, en topología, es el conjunto de puntos que distan de otro (el centro), una distancia igual o menor dada (el radio). Equivale al conjunto de puntos contenidos dento de una superficie esférica, incluida dicha superficie.
Definición y notaciones
Sea (E,d) un espacio pseudométrico (por lo general se toma un espacio métrico, pero basta con que d sea pseudodistancia). Sea un número real r > 0. Sea
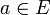. Se define la bola cerrada de centro a y radio r como el conjunto 
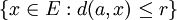.Este conjunto tiene distintas maneras de denotarse. La usual y universal es
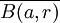, o también 
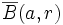. A veces, si en el espacio existen distintas (pseudo-)distancias definidas, se hace hincapié en qué (pseudo)-distancia se está usando para definir el conjunto, utilizando esta notación: 
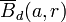. En algunos textos se denota sin embargo por 
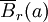.En Análisis Funcional, cuando se trabaja con espacios normados la notación B(a,r) se reserva para las bolas cerradas, usando para las bolas abiertas la notación U(a,r) (con el peligro de confusión que eso genera).
Cuando hablamos de espacios euclídeos, la bola es "redonda", en el sentido intuitivo del término, por lo que la bola de centro a y radio r coincide en esos casos con los puntos encerrados por una superficie esférica (entendiendo que consideramos los puntos de la propia superficie esférica como puntos de la bola). En el caso particular del plano, la figura entonces obtenida (es decir, el conjunto
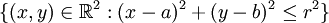) es el disco cerrado de centro (a,b) y radio r, razón por la cual se denota por 
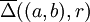. Nótese que esta situación se da en particular en Variable Compleja, siendo entonces la notación 
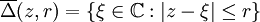(donde | ξ | representa el módulo de ξ). Aunque no es estándar, sí es usual encontrar textos en los que 
denota al disco de radio unidad centrado en el origen, i.e.,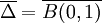 
.Propiedades
Toda bola cerrada es un conjunto cerrado.
El conjunto de todas las bolas cerradas de un espacio seudométrico (
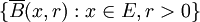) no forman una base de los cerrados de la topología asociada a la seudodistancia.Sin embargo, si consideramos un punto cualquiera del espacio y lo fijamos (por ejemplo, el punto x), el conjunto de bolas cerradas centradas en x (
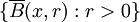) forman una base de entornos de x. En concreto es una base de entornos cerrados, compactos, conexos, conexos por caminos y simplemente conexos. Si el espacio es además un espacio vectorial topológico, también es base de entornos convexos. De hecho, podemos tomar la siguiente base de entornos: 
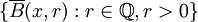que (además de tener todas las propiedades antedichas) es numerable. Esto prueba que todo espacio seudométrico cumple el Primer Axioma de Numerabilidad.Enlaces externos
- Weisstein, Eric W. Ball From MathWorld
- Weisstein, Eric W. Open Ball From MathWorld
- Weisstein, Eric W. Closed Ball From MathWorld
Categorías: Topología | Geometría métrica | Análisis matemático
Wikimedia foundation. 2010.
