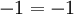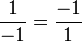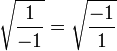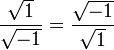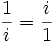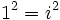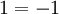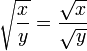En matemáticas, hay múltiples demostraciones matemáticas de contradicciones obvias. A pesar de que las demostraciones son erróneas, los errores son sutiles, y la mayor parte de las veces, intencionados. Estas falacias se consideran normalmente meras curiosidades, pero pueden ser usadas para ilustrar la importancia del rigor en esta área.

La mayoría de estas demostraciones dependen de variantes del mismo error. El error consisten en usar una función f que no es biyectiva, para observar que f(x) = f(y) para ciertas x e y, concluyendo (erróneamente) que por tanto x = y. La división por cero es un caso particular: la función f es x → x × 0, y el paso erróneo es comenzar con x × 0 = y × 0 y con ello concluir que x = y.

Contenido 1 Ejemplos 1.1 Demostración de que 1 equivale a −1 1.2 Demostración de que 1 es menor que 0 1.3 Demostración de que 2 equivale a 1 1.4 Otra demostración de que 2 equivale a 1 1.5 Demostración de que 4 equivale a 2 1.6 Demostración de que a equivale a b 1.7 Demostración de que 0 equivale a 1 2 Véase también

Ejemplos

Demostración de que 1 equivale a −1

Comenzamos con

Ahora, los convertimos en fracciones

Aplicando la raíz cuadrada en ambos lados obtenemos

Que equivale a

Pero ya que 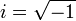(ver número imaginario), podemos sustituirlo, obteniendo

Reordenando la ecuación para eliminar las fracciones, obtenemos

Y ya que i² = − 1 tenemos como resultado

Q.E.D.

Esta demostración no es válida, ya que aplica mal el siguiente principio de las raíces cuadradas:

Este principio sólo es correcto cuando tanto x como y son números positivos. En la "demostración" anterior, una de estas dos variables es un número negativo, lo que invalida toda la demostración.

Demostración de que 1 es menor que 0

Supongamos que

x < 1

Ahora tomamos el logaritmo en ambos lados de la desigualdad. Podemos hacerlo siempre que x > 0, porque los logaritmos crecen monótonamente. Si tenemos en cuenta que el logaritmo de 1 es 0, obtendremos

lnx < 0

Dividir por ln x da como resultado

1 < 0

Q.E.D.

El error se encuentra en el último paso, la división. Este paso es erróneo porque el número por el que estamos dividiendo es negativo, lo que a su vez es porque el argumento del logaritmo es menor que 1, por nuestra suposición original. Una multiplicación o división por un número negativo invierte el símbolo de desigualdad. En otras palabras, deberíamos obtener 1 > 0, lo que es, por cierto, correcto.

(Véase la demostración correcta en "Demostración matemática)".

Demostración de que 2 equivale a 1

Sean a y b dos cantidades iguales. Se sigue que:

a	=	b
a²	=	ab
a² - b²	=	ab - b²
(a - b)(a + b)	=	b(a - b)
a + b	=	b
b + b	=	b
2b	=	b
2	=	1

Q.E.D.

La falacia se encuentra en la línea 5: el paso de la línea 4 a la 5 implica una división por a-b, que es cero ya que a equivale a b (por la suposición). Como la división por cero no está definida, la demostración no es válida."

La otra falacia es que también se demostraría que a = 0, pues si: a + b = b => a = b - b => a = 0

Otra demostración de que 2 equivale a 1

• Por definición de la multiplicación, se tiene que, para x ≠ 0,

  x = 1 + 1 + ... + 1 (x términos)

• Multiplicando ambos lados por x,

  x² = x + x + ... + x (x términos)

• Derivando con respecto a x,

  2x = 1 + 1 + ... + 1 (x términos)

• Ahora bien, volviendo a la primera línea, se ve que el lado derecho de esa igualdad es x, y por lo tanto,

  2x = x

• Dividiendo ambos lados por x (lo cual es posible, pues x ≠ 0), se tiene

  2 = 1

Q.E.D.

El error: en la primera línea de la supuesta demostración se asumió que x era entero; dicha expresión no tiene sentido para números no enteros. Por otro lado, para derivar funciones hace falta un dominio continuo como los reales, no los enteros; para cada x entero se tiene una ecuación correcta, pero para derivar ambos lados hace falta una ecuación de funciones, no de enteros, y la función x + x +... + x "con x términos" no tiene sentido en general (¿cómo se pueden tener x términos?), con lo cual no es derivable.

Demostración de que 4 equivale a 2

4 = 4

Restamos a ambos lados de la ecuación

4 - 4 = 4 - 4

En un lado factorizamos usando la "suma por su diferencia" y en el otro lado se factoriza por 2

(2 - 2) (2 + 2) = 2 (2 - 2)

Cancelamos los términos iguales a cada lado de la ecuación (2 - 2)

(2 + 2) = 2

Nos queda como resultado

4 = 2

Q.E.D.

La falacia se encuentra en el paso de la línea 3 a la 4, ya que implica una división por (2 - 2), que es cero. Como la división por cero no está definida, la demostración no es válida.

Demostración de que a equivale a b

Comenzamos con

a - b = c

Elevamos al cuadrado ambos lados

a² - 2ab + b² = c²

Como (a - b)(c) = c² = ac - bc, podemos reescribirlo como

a² - 2ab + b² = ac - bc

Si lo reordenamos, obtenemos

a² - ab - ac = ab - b² - bc

Factorizamos ambos miembros

a(a - b - c) = b(a - b - c)

Dividimos ambos miembros por (a - b -c)

a(a - b - c) = b(a - b - c)

Al final

a = b

Q.E.D.

La falacia consiste en que si a - b = c, entonces a - b - c = 0, por lo que hemos realizado una división por cero, que invalida la demostración.

Demostración de que 0 equivale a 1

Lo siguiente es una "demostración" de que 0 es igual a 1

0	=	0 + 0 + 0 +...
	=	(1 − 1) + (1 − 1) + (1 − 1) +...
	=	1 + (−1 + 1) + (−1 + 1) + (−1 + 1) +...	(ley asociativa)
	=	1 + 0 + 0 + 0 +...
	=	1

Q.E.D.

El error se encuentra en que la ley asociativa no se puede aplicar libremente a sumas infinitas a menos que sean absolutamente convergentes.

Véase también

• Paradoja