Integral de Fresnel

Integral de Fresnel
S(x) and C(x) El máximo de C(x) es 0,977451424. Si se utiliza πt²/2 en vez de t², entonces la imagen estaría escalada verticalmente y horizontalmente (ver comentario abajo).

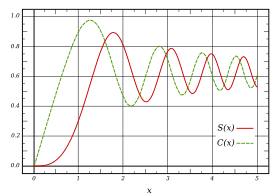
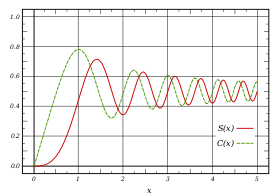
Las integrales de Fresnel, S(x) y C(x), son dos funciones trascendentales que hacen honor a Augustin-Jean Fresnel y que son empleadas en campos que se basan en ecuaciones de ondas, como la óptica. Las mismas se originan al realizar el análisis de fenómenos de difracción de Fresnel en el campo próximo, y se definen según las siguientes expresiones integrales:

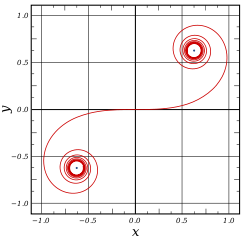
S(x)=\int_0^x \sin(t^2)\,dt,\quad C(x)=\int_0^x \cos(t^2)\,dt.

Las gráficas simultaneas paramétricas de S(x) y C(x) es la espiral de Cornu, o clotoide.

Contenido

Definición

Integrales normalizadas de Fresnel, S(x) y C(x). En estas curvas, el argumento de la funcion trigonometrica es πt²/2, a diferencia de t² en el ejemplo previo.

Las integrales de Fresnel admiten las siguientes expansiones en serie de potencias que convergen para todo x:

S(x)=\int_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!},
C(x)=\int_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}.

Definiciones alernativas

Algunos autores, incluidos Abramowitz y Stegun, (ec 7.3.1 – 7.3.2) utilizan \pi t^2/2 \, como exponente de las integrales que definen a S(x) y C(x). Para obtener las mismas funciones se debe multiplicar la integral por \sqrt{2/\pi} y dividir el argumento x por el mismo factor.

Espiral de Cornu

Espiral de Cornu (x,y)=(C(t), S(t)). La espiral converge al centro de los dos remolinos extremos de la imagen, a medida que t tiende a más infinito y menos infinito.

La espiral de Cornu, también conocida como clotoide, es la curva cuyas ecuaciones paramétricas vienen dadas por S(t) y C(t). La espiral de Cornu fue creada por Marie Alfred Cornu como un nomograma para los cálculos de difracción óptica.

Puesto que:

C'(t)^2 + S'(t)^2 = \sin^2(t^2) + \cos^2(t^2) = 1\,

en esta parametrización el vector tangente tiene longitud unitdad y t es la longitud de arco medida a partir de (0,0) (e incluyendo signo), de lo que se deduce que la curva tiene longitud infinita.

Además la espiral de Cornu tiene la propiedad de su curvatura en cualquier punto es proporcional a la distancia a lo largo de la curva medida desde el origen. Esta propiedad hace que sea útil como curva de transición en el trazado de autopistas o ferrocarriles, puesto que un vehículo que siga dicha curva a velocidad constante tendrá una aceleración angular constante. Igualmente las secciones de esta espiral clotoide son usadas comúnmente en montañas rusas por lo que algunas vueltas completas se conocen como loops "clotoides".


Propiedades

  • Utilizando las expansiones en series de potencias indicadas previamente, se puede extender las integrales de Fresnel al dominio de los números complejos, obteniendo de esta manera funciones analíticas de una variable compleja. Las integrales de Fresnel se pueden expresar utilizando la función error mediante las siguientes expresiones:
S(x)=\frac{\sqrt{\pi}}{4} \left( \sqrt{i}\,\operatorname{erf}(\sqrt{i}\,x) + \sqrt{-i}\,\operatorname{erf}(\sqrt{-i}\,x) \right)
C(x)=\frac{\sqrt{\pi}}{4} \left( \sqrt{-i}\,\operatorname{erf}(\sqrt{i}\,x) + \sqrt{i}\,\operatorname{erf}(\sqrt{-i}\,x) \right).
  • Excepto en casos especiales no es posible evaluar a las integrales que definen C(x) y S(x) en forma cerrada. Los límites de estas funciones cuando x tiende a infinito son:
\int_{0}^{\infty} \cos t^2\,dt = \int_{0}^{\infty} \sin t^2\,dt = \frac{\sqrt{2\pi}}{4} = \sqrt{\frac{\pi}{8}}.

Valores particulares

  • S(0) = C(0) = 0\,
  • S(\infty) = C(\infty) = \frac{1}{\sqrt{2\pi}}

Véase también

Referencias

  • R. Nave, The Cornu spiral, Hyperphysics (2002) (Uses πt²/2 instead of t².)
  • Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 7)
  • «Roller Coaster Loop Shapes». Consultado el 13-08-2008.

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Fresnel (disambiguation) — Fresnel can refer to physicist Augustin Jean Fresnel, or to the following topics associated with him:*Fresnel equations, describing light reflection and refraction *Huygens Fresnel principle, a description of wave propagation *Fresnel diffraction …   Wikipedia

  • Fresnel diffraction — In optics, the Fresnel diffraction equation for near field diffraction, is an approximation of Kirchhoff Fresnel diffraction that can be applied to the propagation of waves in the near field.[1] The near field can be specified by the Fresnel… …   Wikipedia

  • Fresnel integral — S(x) and C(x) The maximum of C(x) is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally (see below). Fresnel integrals, S(x) and C(x), are two transcendental functions named aft …   Wikipedia

  • Fresnel-Integral — Als Fresnel Integrale werden in der Mathematik die beiden uneigentlichen Integrale bezeichnet; sie ergeben sich aus dem gaußschen Fehlerintegral unter Benutzung des cauchyschen Integralsatzes. Fresnel kannte sie um 1819. Euler kannte schon 1781… …   Deutsch Wikipedia

  • Fresnel equations — The Fresnel equations, deduced by Augustin Jean Fresnel (pronEng|freɪˈnɛl), describe the behaviour of light when moving between media of differing refractive indices. The reflection of light that the equations predict is known as Fresnel… …   Wikipedia

  • Fresnel zone — In optics and radio communications, a Fresnel zone (pronounced FRA nel Zone ), named for physicist Augustin Jean Fresnel, is one of a (theoretically infinite) number of concentric ellipsoids of revolution which define volumes in the radiation… …   Wikipedia

  • Fresnel-Beugung — Das Beugungsintegral ermöglicht es, in der Optik die Beugung von Licht durch eine beliebig geformte Blende zu berechnen. Speziell wird dabei, ausgehend von einer einfallenden Elementarwelle und der Blendenfunktion, die die Lichtdurchlässigkeit… …   Deutsch Wikipedia

  • Fresnel number — The Fresnel number F , named after the physicist Augustin Jean Fresnel, is a dimensionless number occurring in optics, in particular in diffraction theory.For an electromagnetic wave passing through an aperture and hitting a screen, the Fresnel… …   Wikipedia

  • Fresnel-Zahl — Die Fresnel Zahl F, benannt nach dem Physiker Augustin Jean Fresnel, ist eine dimensionslose Kennzahl, die in der Optik, besonders bei der Beugung, Verwendung findet. Sie beschreibt, wie stark die Beugung eines Lichtstrahls an einer Blende ist.… …   Deutsch Wikipedia

  • Integral de caminos (mecánica cuántica) — Cualquier posible trayectoria entre A y B contribuye a la probabilidad de que una partícula se propague entre ambos puntos. La formulación mediante integral de caminos de la mecánica cuántica es un enfoque en el que las relaciones fundamentales… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”