Integral de Gauss

Integral de Gauss
Función gaussiana \scriptstyle e^{-x^2}. El área encerrada bajo esa curva con el eje x es \scriptstyle \int_{-\infty}^\infty e^{-x^2}\,dx = \sqrt{\pi}.

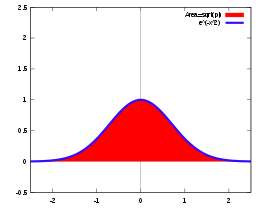
En matemáticas la integral de Gauss, integral gaussiana o integral de probabilidad, es la integral impropia de la función gaussiana e^{{-x}^2} sobre toda la recta de los reales. Debe su nombre al matemático y físico alemán Carl Friedrich Gauss, y su valor es:

\int_{-\infty}^\infty e^{-x^2}\,dx = \sqrt{\pi}

Esta integral tiene amplias aplicaciones, incluyendo normalización, en teoría de la probabilidad y transformada continua de Fourier. También aparece en la definición de la función error. A pesar de que no existe ninguna función elemental para la función error, como se puede demostrar mediante el algoritmo de Risch, la integral Gaussiana puede ser resuelta analíticamente con las herramientas del cálculo. O sea, no existe una integral indefinida elemental para \int e^{-x^2}\,dx, pero si es posible evaluar la integral definida\int_{-\infty}^\infty e^{-x^2}\,dx.

Contenido

Cálculo de la integral

La forma más común de calcular la integral de Gauss en el plano R2 es mediante la integración doble en el sistema cartesiano de coordenadas, para después hacer un cambio de coordenadas a coordenadas polares y calcular el valor. Se procede de la siguiente manera:


\begin{align} \int_{\mathbb{R}^2} e^{-(x^2+y^2)}\,dx\,dy &= \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-(x^2+y^2)}\,dx\,dy\\ &= \left ( \int_{-\infty}^\infty e^{-x^2}\,dx \right ) \cdot \left ( \int_{-\infty}^\infty e^{-y^2}\,dy \right )\\ &= \left ( \int_{-\infty}^\infty e^{-x^2}\,dx \right )^2 \end{align}



\begin{align} \int_{\mathbb{R}^2} e^{-(x^2+y^2)}\,dx\,dy &= \int_0^{2\pi} \int_0^{\infin} re^{-r^2}\,dr\,d\theta\\ &= 2\pi \int_0^\infty re^{-r^2}\,dr\\ &= 2\pi \int_{-\infty}^0 \frac{1}{2} e^s\,ds = \pi \int_{-\infty}^0 e^s\,ds = \pi (e^0 - e^{-\infty}) = \pi (1 - 0) = \pi, \end{align}


donde el factor r es consecuencia de calcular el determinante del cambio de las coordenadas cartesianas a polares, y s aparece al hacer un cambio de variable tal que s = - r2, ds = -2rdr. Así pues, obtenemos:

\int_{\mathbb{R}^2} e^{-(x^2+y^2)}\,dx\,dy = \left ( \int_{-\infty}^\infty e^{-x^2}\,dx \right )^2 = \pi

por lo tanto

\int_{-\infty}^\infty e^{-x^2}\,dx = \sqrt{\pi}

Relación con la función gamma

Puesto que la integral gaussiana es una función par


\int_{-\infty}^{\infty} e^{-x^2} dx = 2 \int_0^\infty e^{-x^2} dx

lo cual, después de hacer un cambio de variable, se convierte en la Integral:

\int_0^\infty e^{-t} \ t^{-1/2} dt \, = \, \Gamma\left(\frac{1}{2}\right)

donde Γ es la función gamma. Esto muestra por qué el factorial de la mitad de un entero es un número racional múltiplo de \textstyle \sqrt \pi. Más generalmente

\int_0^\infty e^{-ax^b} dx = a^{-1/b} \, \Gamma\left(1+\frac{1}{b}\right).

Generalizaciones

La integral de cualquier función Gaussiana es reducible en termino de la integral Gaussiana

\int_{-\infty}^{\infty} ae^{-(x+b)^2/c^2}\,dx.

la constante a puede ser factorizada fuera de la integral. Reemplazando x con y - b nos da:

a\int_{-\infty}^\infty e^{-y^2/c^2}\,dy.

sustituyendo y con cz nos da:

a|c|\int_{-\infty}^\infty e^{-z^2}\,dz = a|c|\sqrt{\pi}.

Referencias


Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Gauss–Kronrod quadrature formula — In numerical mathematics, the Gauss–Kronrod quadrature formula is a method for numerical integration (calculating approximate values of integrals). Gauss–Kronrod quadrature is a variant of Gaussian quadrature, in which the evaluation points are… …   Wikipedia

  • Gauss — Saltar a navegación, búsqueda Gauss se puede referir a: El matemático y físico Carl Friedrich Gauss; La unidad de medida de campo magnético gauss. Términos relacionados: La distribución de Gauss o distribución normal es una distribución de… …   Wikipedia Español

  • Gauss' law for gravity — In physics, Gauss law for gravity, also known as Gauss flux theorem for gravity, is a law of physics which is essentially equivalent to Newton s law of universal gravitation. Its form is mathematically similar to Gauss law for electricity; in… …   Wikipedia

  • Gauss's law — In physics, Gauss s law, also known as Gauss s flux theorem, is a law relating the distribution of electric charge to the resulting electric field. It is one of the four Maxwell s equations, which form the basis of classical electrodynamics, and… …   Wikipedia

  • Gauss–Bonnet theorem — The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry (in the sense of curvature) to their topology (in the sense of the Euler characteristic). It is named …   Wikipedia

  • Gauss's law for magnetism — In physics, Gauss s law for magnetism is one of Maxwell s equations, the four equations that underlie classical electrodynamics. It states that the magnetic field B has divergence equal to zero, in other words, that it is a solenoidal vector… …   Wikipedia

  • Integral — This article is about the concept of integrals in calculus. For the set of numbers, see integer. For other uses, see Integral (disambiguation). A definite integral of a function can be represented as the signed area of the region bounded by its… …   Wikipedia

  • Gauss's lemma (polynomial) — This article is about Gauss s lemma for polynomials. See also Gauss s lemma. In algebra, in the theory of polynomials, Gauss s lemma, named after Carl Friedrich Gauss, is either of two related statements about polynomials with integral… …   Wikipedia

  • Gauss (unit) — The gauss, abbreviated as G, is the cgs unit of measurement of a magnetic field B (which is also known as the magnetic flux density , or the magnetic induction ), named after the German mathematician and physicist Carl Friedrich Gauss. One gauss… …   Wikipedia

  • Gauss-Verteilung — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… …   Deutsch Wikipedia

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”