- Polinomios ortogonales
-
Polinomios ortogonales
Los polinomios ortogonales son conjuntos de polinomios que forman una base ortogonal son importantes porque aparecen en la teoría de ecuaciones diferenciales, muy especialmente en la teoría de Sturm-Liouville, la teoría de espacios de Hilbert, la teoría de la aproximación de funciones y la mecánica cuántica.
Espacios de Hilbert
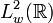
La mayoría de las familias
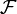de polinomios ortogonales más usados son bases ortogonales de un espacio de Hilbert 
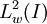de funciones de cuadrado integrable respecto al producto escalar con función de ponderación 
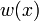. Es decir: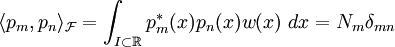
Donde:
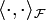es el producto escalar del espacio .
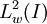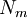es un factor de normalización que vale 1 si la familia de polinomios es además ortonormal.
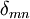es el delta de Kronecker.
Además estos polinomios suelen ser los vectores propios de un operador diferencial lineal autoadjunto de segundo orden u operador Sturm-Liouville de la forma:
![\mathcal{L}(y) =
\frac{1}{w}\left[ -\frac{d}{dx}\left[p(x) \frac{dy}{dx} \right] + q(x) y \right]](/pictures/eswiki/101/e63877cb2bac9f852ab88cb1474d1f4c.png)
Ejemplos
- Los polinomios de Legendre son soluciones de la ecuación diferencial:
![(1-x^2)y'' -2xy' +n(n+1)y = 0, \qquad y(x) = P_n(x)
= \frac{1}{2^n} \frac{d^n}{dx^n} (1-x^2)^n, \qquad \{w = 1, I = [-1,1]\}](/pictures/eswiki/54/65c86b0f6461111a8267ec834e8b1842.png)
- Los polinomios de Hermite son soluciones de la ecuación diferencial:
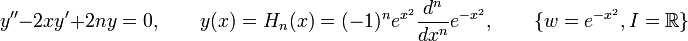
- Los polinomios de Laguerre son soluciones de la ecuación diferencial:
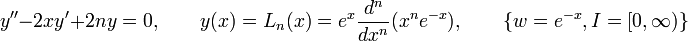
Mecánica cuántica
En mecánica cuántica son de uso común las siguientes familias de polinomios ortogonales:
- Los polinomios de Hermite aparecen en mecánica cuántica como soluciones del oscilador armónico unidimensional.
- Los polinomios de Legendre y sus funciones asociadas aparecen en problemas cuánticos con simetría esférica, ya que los armónicos esféricos son funciones ortogonales sobre la esfera expresables mediante estos polinomios.
Categoría: Funciones especiales
Wikimedia foundation. 2010.
