- Área de un círculo
-
El área de un círculo, es la medida de la superficie limitada por la circunferencia del círculo dado.
siendo
el área, y 
el radio del círculo.Contenido
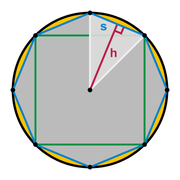
Área del círculo como superficie interior del polígono de infinitos lados
El área de un círculo se deduce sabiendo que la superficie interior de cualquier polígono regular es igual al producto entre el apotema y el perímetro de este polígono, es decir:
.Si se considera la circunferencia como el polígono regular de infinitos lados, entonces el apotema coincide con el radio de la circunferencia y el perímetro con la longitud de la circunferencia. Por tanto el área interior es:
Área del círculo como superficie trianglular
Círculo desplegado para conformar un triángulo.
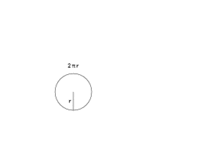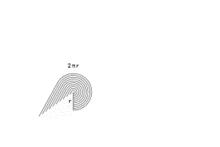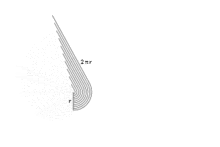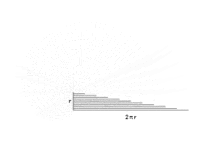
Si en un círculo desplegamos todos sus anillos circulares, y los consideramos como rectángulos, se forma un triángulo rectángulo de altura r y base 2πr (siendo la longitud de la base la de la circunferencia perimetral).
El área A de este triángulo de altura r, será:
Otras demostraciones
Para representar una función que describa una circunferencia, debe definirse una nueva función
, como la unión de otras dos funciones. De lo contrario, se contradice la definición de función que dice que a cada 
del dominio de una función 
, le corresponde un único 
en el recorrido de . Así, podemos definir los puntos pertenecientes a la Circunferencia y calcular su área por medio de integrales.Para ello, primero daremos una base que muestre cómo se puede construir una ecuación de la circunferencia
Distancia entre dos puntos de un plano
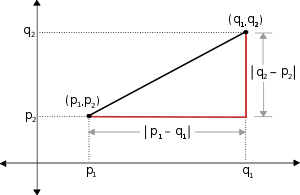Plano, Construcción de la Circunferencia.Según el Teorema de Pitágoras, se puede establecer una relación que describa de manera algebraica la distancia que existe entre dos puntos
y 
del plano:- Sean y , dos puntos en el plano, tales que
y
con
, 
, 
y 
números reales cualesquiera. (Ver Figura)- Por el teorema de Pitágoras, tenemos que
donde d es la distancia entre los dos puntos
y .Ecuación de la circunferencia perimetral
Por definición, una circunferencia es el lugar geométrico del conjunto de los puntos
que equidistan de un punto 
, llamado centro de la circunferencia.Formalizando esto, podemos escribir como conjunto, todos estos puntos:
como
y además
y
(para que no sea un punto),entonces
y podemos concluir que
Esto es para aclarar que al elevar al cuadrado, no se están agregando soluciones a nuestra ecuación.
- Comúnmente se escribe la ecuación de la circunferencia como sigue
donde
es el centro de la circunferencia.Nótese que esto no es una función, ya que no cumple con los requisitos de ésta.
Hemos definido entonces, el conjunto
que contiene todos los puntos que describen una circunferencia.Circunferencia en el plano de ejes ortogonales
Dijimos anteriormente que nuestra expresión, no podía ser una función. Entonces, podemos crear una nueva función
que sea la unión del conjunto de puntos de 
y 
, donde y describen semicircunferencias. Esto es,
,
Se usan estas funciones para calcular el área de de un círculo.Cálculo del área de un círculo
Las integrales están directamente relacionadas con el cálculo de áreas de funciones, siendo nuestra herramienta fundamental en el cálculo del área del círculo.
Las funciones
y son monótonas y acotadas en el intervalo ![\mathit{[-r,r]} \,\!](c/38c389c0eee942f3ec03393ec24cc0c3.png)
, por lo que cada una es integrable en ese intervalo.El área comprendida entre
y es el área del círculo, y se calcula como sigue:![A(r) = \int_{-r}^{r} {[g(x)-f(x)]}\, dx \,\!](c/7fc62303c755b51e9fdd14dd0365d4f9.png)
donde
es el área del círculo.Como
, podemos reescribir lo anterior obteniendo
.
En particular, cuando
se tiene la igualdad
.
Cambiando la escala en el eje y aplicando el Teorema de dilatación o contracción del intervalo de integración, tenemos, usando 
, que
Luego,
Es decir,
Se define
, como el área del círculo unidad. Con esta definición podemos decir que:
Véase también
-
Wikimedia foundation. 2010.
