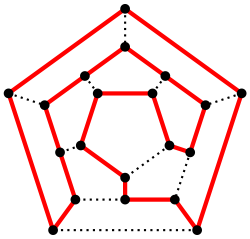
- Camino hamiltoniano
-
En el campo matemático de la teoría de grafos, un camino hamiltoniano en un grafo es un camino, una sucesión de aristas adyacentes, que visita todos los vértices del grafo una sola vez. Si además el último vértice visitado es adyacente al primero, el camino es un ciclo hamiltoniano.
El problema de encontrar un ciclo (o camino) hamiltoniano en un grafo arbitrario se sabe que es NP-completo.
Los caminos y ciclos hamiltonianos fueron nombrados después que William Rowan Hamilton, inventor del juego de Hamilton, lanzara un juguete que involucraba encontrar un ciclo hamiltoniano en las aristas de un grafo de un dodecaedro. Hamilton resolvió este problema usando cuaterniones, pero esta solución no se generaliza a todos los grafos.
Contenido
Definición
Un camino hamiltoniano es un camino que pasa por cada vértice exactamente una vez. Un grafo que contiene un camino hamiltoniano se denomina un ciclo hamiltoniano o circuito hamiltoniano si es un ciclo que pasa por cada vértice exactamente una vez (excepto el vértice del que parte y al cual llega). Un grafo que contiene un ciclo hamiltoniano se dice grafo hamiltoniano.
Estos conceptos se pueden extender para los grafos dirigidos.
Ejemplos
- El grafo completo con más de 2 vértices es hamiltoniano.
- Todos los grafos ciclos son hamiltonianos.
- Todos los sólidos platónicos, considerados como grafos, son hamiltonianos.
Notas
Cualquier ciclo hamiltoniano puede ser convertido en un camino hamiltoniano si se remueve cualquiera de sus aristas, pero un camino hamiltoniano puede ser extendido en ciclo sólo si los vértices de los extremos son adyacentes.
Teorema de Bondy-Chvátal
La mejor caracterización de los grafos hamiltonianos fue dada en 1972 por el teorema de Bondy-Chvátal que generalizaba los resultados anteriormente encontrados por G. A. Dirac. Básicamente dice que un grafo es hamiltoniano si existen suficientes aristas. Primero debemos definir lo que es la cerradura de un grafo.
Dado un grafo G con n vértices, la cerradura (cl(G)) es construida de manera única a partir de G agregando toda arista u-v si el par no adyacente de vértices u y v cumple que grado(v) + grado(u) ≥ n
Un grafo es hamiltoniano si y sólo si su grafo cerradura es hamiltoniano.
Bondy-Chvátal (1972)Como todos los grafos completos son hamiltonianos, todos los grafos cuya cerradura sea completa son hamiltonianos. Este resultado se basa en los teoremas de Dirac y Ore.
Un grafo con n vértices (n > 3) es hamiltoniano si cada vértice tiene grado mayor o igual a n/2.
Dirac (1952)Un grafo con n vértices (n > 3) es hamiltoniano si la suma de los grados de 2 vértices no adyacentes es mayor o igual que n.
Ore (1960)Sin embargo, existe un resultado anterior a todos estos teoremas.
Un grafo con n vértices (n ≥ 2) es hamiltoniano si la suma de los grados de 2 vértices es mayor o igual que n-1.
L.Redei (1934)Como puede verse, este teorema pide más hipótesis que los anteriores ya que la propiedad de los grados debe cumplirse para todo vértice en el grafo.
Wikimedia foundation. 2010.